Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 72

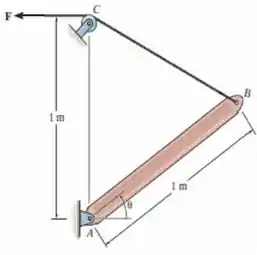
A lança tem peso uniforme de 3   k N e é alçada até a posição desejada por meio do cabo B C . Se o cabo tiver diâmetro de 15   m m , construa um gráfico da tensão normal média no cabo em função da posição da lança θ para 0 ° ≤ θ ≤ 90 ° .

Passo 1

Vamos analisar, primeiramente, o ângulo B que é um dos ângulos da base do triângulo ABC que é isósceles, ou seja, vamos ter:

2 ϕ b + C = 180 °   e   C + θ = 90 ° → C = 90 ° - θ  

Substituindo o ângulo C na primeira equação vamos obter

2 ϕ b + 90 ° - θ = 180 ° → ϕ b = 45 ° + θ 2

Saber sobre esse ângulo vai ser importante para gente conseguir decompor a força F mostrada na figura.

Feitas essas considerações vamos lembrar como se calcula a tensão normal média , basta seguir a seguinte fórmula:

σ m e d = P A  

Com

P: resultante da força normal;

A: Área da seção transversal;

Passo 2

Para o suporte A como temos um apoio que restringe 2 graus de liberdade vamos ter que duas forças de reação: uma vertical e uma horizontal que denotaremos por A y   e   A x , dessa forma, vamos ter

∑ M a = 0 → F b c ⋅ s e n ϕ b ⋅ 1 m - 3 k N ⋅ 0,5 m ⋅ cos ⁡ θ = 0

F b c = 1,5 k N ⋅ cos ⁡ θ s e n   45 ° + θ 2

Passo 3

σ b c = F b c A b c

Sendo

A b c = π ⋅ d 0 2 4

Teremos

σ b c = 1,5 k N ⋅ cos ⁡ θ s e n   45 ° + θ 2 π ⋅ d 0 2 4 = 6 k N π ⋅ d 0 2 ⋅ cos ⁡ θ s e n   45 ° + θ 2

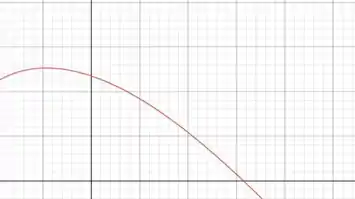
Plotando o gráfico dessa função vamos ter

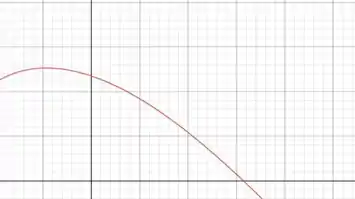
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra tem área de seção transversal A e está submetida à carga axial P . Detetmine a tensão normal média e a tensão de cisalhamento média que agem na seção sombreada que está orientada a um ângulo θ
O elemento A da junta escalonada de madeira usada na treliça está submetido a uma força de compressão de 5k N . Determine a tensão normal média que age na haste do pendural C com diâmetro de 10m m e n
A coluna é feita de concreto de densidade 2,30M g / m 3 e está sujeita a uma força de compressão axial de 15k N em sua extremidade superior B . Determine a tensão normal média na coluna em função da d
O raio do pedestal é definido por r=( 0,5 ⋅ e - 0.008 y 2 )m , onde y é dado em metros. Se o material tiver densidade de 2,5M g / m 3 , determine a tensão normal média no apoio.