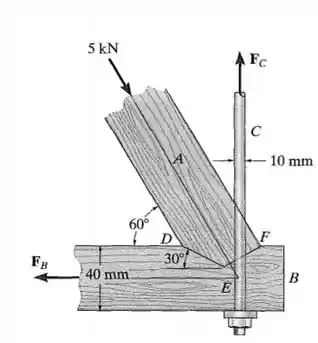
O elemento da junta escalonada de madeira usada na treliça está submetido a uma força de compressão de . Determine a tensão normal média que age na haste do pendural com diâmetro de e no elemento com espessura de .
Passo 1
Falaa! Bora!
Antes de partirmos para a resolução vamos anotar todos os dados que foram fornecidos, contando também com as informações dadas de maneira implícita no enunciado. Dessa forma, teremos
- Área em B é um retângulo e é dada por: ;
- Área da seção do pendural que contem C é dada por:
- A força de aplicada no elemento A da junta pode ser decomposto em uma componente horizontal e uma componente vertical (da decomposição de vetores) expressos como:
Repara que a gente usou que é o ângulo da linha de ação da força com a horizontal. Não confundi com o ângulo de que só está representando um ângulo interno de construção da estrutura.
E com isso tudo, a gente quer a força normal média na haste e no elemento . Que tem essa fórmulinha:
A gente já achou as áreas para cada seção. Então nosso problema aqui é achar as forças aplicadas em cada seção e , beleza? Vamos lá!
Passo 2
Vamos aplicar os somatórios das forças iguais a 0 para as direções horizontais (eixo ) e verticais (eixo ), assim, ficaremos com
Olha só! Achamos as forças em cada seção.
Passo 3
Agora é aplicar a fórmulinha da tensão normal que a gente viu no passo 1:
Atenção nas unidades. Como a gente dividiu por , nossa resposta já sai em .
Prontinho!