Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 78
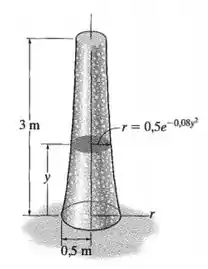
O raio do pedestal é definido por , onde é dado em metros. Se o material tiver densidade de , determine a tensão normal média no apoio.
Passo 1
E aí meus consagrados, como vocês estão? Prontos pra mais uma questão?
Primeiramente vamos encontrar o que queremos encontrar nessa questão: buscamos encontrar o valor da tensão normal na base do nosso pedestal utilizando os dados que nos foram fornecidos no enunciado que podemos transcrevê-las aqui como
Lembrando que tensão normal é dada pela resultante da força que atua na seção transversal do objeto em questão dividido pela área da seção transversal que vamos definir por que pode ser definida como
Pensa comigo: como queremos a tensão na base do pedestal, e a gente já tem a área, precisamos achar o que? A força que atua na seção transversal da base do pedestal! E quem é ela? Podemos dizer que ela é a força de reação no pedestal.
E qual é o valor dessa força? É o mesmo valor da força peso do pedestal! Então é ela que a gente vai achar!
Passo 2
Ele nos deu a densidade do pedestal. Por ela a gente acha a massa do pedestal e assim a força peso. Maaas, nosso raio é variável, então vamos ter que usar umas paradinhas de cálculo aqui, beleza?
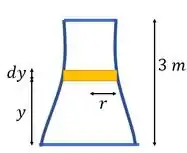
Pensa que a gente tem um disco em , como no desenho. Ele é bem fino, tem espessura . O raio dele vale . Qual vai ser o volume desse disco? Como ele é fininho, vamos chamar esse volume de . Aí concorda que
E como :
Passo 3
Até aí, tudo bem? Agora pensa comigo. O pedestal tem altura . Então a gente pode dizer que:
E aí a gente pode usar esse intervalo e montar uma integral com a expressão do passo anterior!
Integrando ambos os lados dela e colocando os extremos de integração, vamos obter
Essa integral não tem resposta analítica. Se resolve utilizando as funções especiais e nesse caso vamos ter a função gama incompleta: , cujo valor é tabelado. Ou a gente pode usar métodos numéricos para calcular ou uma calculadora/software, belezinha?
Dessa forma, vamos encontrar como resultado para esse volume o seguinte valor:
Passo 4
Como foi dada a densidade do material no enunciado e temos o volume podemos encontrar o valor do peso que será dado por
Agora, ficou simples resolvermos o problema pois nossa tensão normal média será dada por
Pronto, acabou o problema. Uhul!