Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 13
Determine a resultante das forças internas normal e de cisalhamento no elemento em: seção e seção , sendo que cada uma delas passa pelo ponto . Considere . A carga de é aplicada ao longo do eixo do centroide do elemento.
Passo 1
a) Oláaaa, querido! Tá bem?
Então, ele quer saber as forças internas resultantes normal e de cisalhamento que atuam na seção . Para fazer esse tipo de questão, a primeira coisa é cortar nossa peça na seção que ele pediu, escolher um lado e fazer o diagrama de corpo livre da situação nova.
Vamos cortar nosso elemento em e olhar só para cima. Assim:
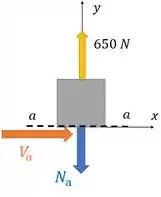
Aí percebe que a gente posiciona nessa seção vetores que representam essas forças internas. A força normal que deve ser perpendicular a seção , e a força de cisalhamento que deve ser paralela a seção.
O sentido dos vetores aqui é mais arbitrário mesmo, tá? Cê escolhe. O importante é respeitar os referenciais que escolher nas continhas. Vamos seguir!
Passo 2
Agora é utilizar as equações de equilíbrio nas duas direções e achar e . Para a vertical:
E para a horizontal:
Passo 3
b) Ele quer a mesma coisa do item anterior, mas agora a seção é inclinada .
Para a seção é só repetir o mesmo processo. Porém, decompondo o par de reação da força de 650 N que age na seção em relação aos nossos novos eixos e
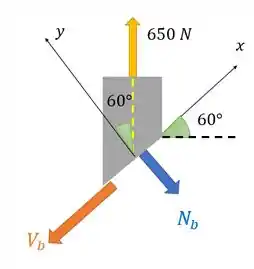
Aplicando as equações de equilíbrio:
Já para o eixo :
Percebe que a gente colocou e na direção das forças que a gente queria porque aí só tivemos que decompor a força de .