Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 54

A área da seção transversal da escora de alumínio tem forma de cruz. Se ela for submetida ao momento M   =   8   k N . m , determine a tensão de flexão que age nos pontos A e B e mostre os resultados em elementos de volume localizados nesses pontos.

Passo 1

Primeiro, vamos calcular o momento de inércia:

I = 0,02 × 0,22 3 12 + 2 × 0,05 × 0,02 3 12 = 1,7813 × 10 - 5 m 4

Calculando-se as tensões, teremos:

σ a = 8 × 10 3 × 0,11 1,7813 × 10 - 5 = 49,4 M P a   C

σ b = 8 × 10 3 × 0,01 1,7813 × 10 - 5 = 4,49 M P a   T

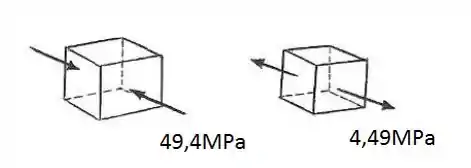
Desenhando os elementos A e B, respectivamente:

Resposta

σ a = 49,4 M P a   C

σ b = 4,49 M P a   T

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma barra de seção transversal circular cheia, com diâmetro d e feita de aço, está vinculada, conforme mostra a figura. Sabendo que para o aço ρ = 7697 k g m 3 , determine o menor diâmetro d que pode
Usando o método da Seção 5.2 , resolva o Problema 5.1 a .Para a viga e carregamento mostrados, ( a ) trace os diagramas de força cortante e momento fletor e ( b ) determine as equações das curvas de f
Determine (a) a distância a para a qual o valor absoluto do momento fletor na viga é o menor possível e (b) a tensão normal máxima correspondente provocada pelo momento fletor. (ver sugestão do proble
Resolva o problema 5.29 considerando P = 480 N e Q = 320 N .
Trace os diagramas de força cortante e momento fletor para a viga e carregamento mostrados na figura, e determine a tensão normal máxima gerada pelo momento fletor.