Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 32
Uma barra de seção transversal circular cheia, com diâmetro e feita de aço, está vinculada, conforme mostra a figura. Sabendo que para o aço determine o menor diâmetro que pode ser utilizado para que a tensão normal provocada pelo momento fletor não ultrapasse
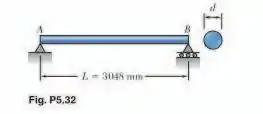
Passo 1
Fala aí, galerinha. Tudo bem com vocês? Bora fazer mais uma questão.
Como temos a massa específica, podemos obter o peso da barra com o volume. O volume será:
Logo:
Por simetria, temos que:
Passo 2
A fórmula da tensão é:
Onde é a distância da linha neutra e o momento de inércia. Para este caso:
Logo:
Passo 3
Portanto, basta substituir os valores encontrados e determinar o Sabemos que:
Logo:
Resolvendo e isolando
Resposta
Exercícios de Livros Relacionados
Uma barra prismática AB é feita de um aço que considerado ser elastoplásticos com E =200 GPa e σ e = 250M P a . Sabendo-se que M = 450N m , determinar (a) a espessura do núcleo elático (b) o raio de c
A barra prismática é feita de um aço que é considerado ser elastoplásticos com E=200GPa e σ e = 250M P a . Para um momento de 150 Nm, paralelo ao eixo z e aplicado na extremidade B, como mostrado, det
Uma viga de seção transversal mostrada é feita de um aço que é considerado ser elastoplásticos, com E=200GPa e σ e = 300M P a . Por flexão em torno do eixo z , determinar o momento fletor e o raio de
Uma viga de seção transversal mostrada é feita de um aço que é considerado elastoplásticos com E = 200G P a e σ e = 240M P a . Por flexão em torno do eixo z, determinar o momento fletor e o raio de cu
Resolva o Prob 4.74 considerando que M = 550N m s