Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 108

Devido a um erro de fabricação, o círculo interno do tubo é excêntrico em relação ao círculo externo. Qual é a porcentagem de redução da resistência à torção quando a excentricidade e é igual a diferença entre os raios

Passo 1

O enunciado nos trás várias informações importantes.

Primeiro ela nos informa que vamos trabalhar com duas configurações de tubo: Um concêntrico e o outro excêntrico.

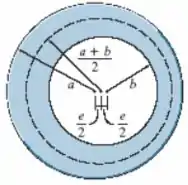
Segundo, ele nos dá uma relação para a excentricidade: e = 1 4 ( a - b )

Terceiro, nos informa o que a questão quer: A porcentagem de redução de resistência.

Por fim, a pegadinha dessa questão está em perceber que a espessura da parede excêntrica varia. Assim é preciso ter cuidado ao aplicar a Equação de Tensão de Cisalhamento

Passo 2

Precisamos relacionar as medidas entre si. Ou seja, precisamos, de alguma forma relacionar a espessura das paredes e o raio médio com a e b .

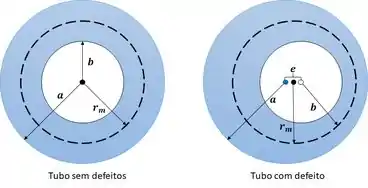
Analisando o tubo sem defeitos podemos definir a espessura de sua parede:

t = a - b

Com a espessura podemos definir o raio médio:

r M = b + 1 2 t

r M = b + a - b 2

r M = a + b 2

Analisando o tubo com defeito, vemos que sua espessura varia por causa da excentricidade. Fazendo uma análise dos raios podemos identificar a espessura da parede.

A espessura mínima é:

a = e + b + t m i n

t m i n = a - e - b

A questão nos dis que a excentricidade é: e = 1 4 ( a - b ) . Aplicando isso na expressão de espessura:

t m i n = a - 1 4 ( a - b ) - b

t m i n = 3 4 ( a - b )

Passo 3

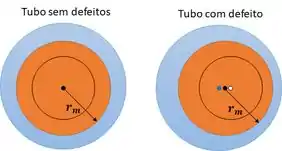
Inicialmente, precisamos calcular a área interna média. Observe que apesar do centros estarem deslocados, a área interna média dos dois tubos é a mesma, destacada em laranja na figura abaixo.

A M = π r M 2

A M = π a + b 2 2

Passo 4

Calculamos agora o torque máximo que pode atuar no tubo sem defeitos. Basta aplicar a equação 5.18:

τ a d m = T 1 2 ⋅ t ⋅ A m

T 1 =   τ a d m ⋅ 2 ⋅ t ⋅ A m

T 1 =   τ a d m ⋅ 2 ⋅ a - b ⋅ π a + b 2 2

Passo 5

Agora vamos calcular o torque máximo que atua no tubo excêntrico.

Vamos considerar o ponto de maior fragilidade do tubo excêntrico, que é o ponto onde a espessura é mínima.

τ a d m = T 2 2 ⋅ t m i n ⋅ A m

T 2 =   τ a d m ⋅ 2 ⋅ t m i n ⋅ A m

T 2 =   τ a d m ⋅ 2 ⋅ 3 4 a - b ⋅ π a + b 2 2

Passo 6

Agora vamos resolver a questão! Vamos ver qual é a relação que existe entre os dois torques:

T 2 T 1 = τ a d m ⋅ 2 ⋅ 3 4 a - b ⋅ π a + b 2 2 τ a d m ⋅ 2 ⋅ a - b ⋅ π a + b 2 2

T 2 T 1 = 3 4 = 0,75 = 75 %

Ou seja, o torque máximo sobre o tubo mal fabricado é 75% do torque possível no tubo bem fabricado, o que significa uma redução de resistência de 25%

Resposta

Redução de resistência = 25 %

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma barra de alumínio AB (G=26 GPa) é ligada a uma barra de latão (G=39 GPa). Sabendo-se que o trecho CD da barra é vazado e tem um diâmetro interno de 40 mm, determinar o ângulo de torção em A.
O arranjo mostrado de eixos com polias para correias planas é usado para transmitir 2 kW do ponto A para o ponto D. Pede-se (a) usando uma tensão de cisalhamento média de 70 Mpa, determinar a velocida
O eixo composto mostrado é torcido pela aplicação do torque T na extremidade A. Sabendo-se que a máxima tensão de cisalhamento na camisa de alumínio é de 60 MPa e que G = 77GPa, para o aço, e G = 26 G
Dois eixos maciços de alumínio (G = 26 GPa) são conectados pelas engrenagens mostradas. Sabendo-se que as extremidades B e D são impedidas de girar, para o carregamento dado determinar a máxima tensão
O eixo maciço mostrado é feito de um aço doce, que é considerado ser elastoplástico com G = 77 GPa e τ=150 MPa. Determinar a correspondente tensão de cisalhamento máxima.