Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 106
O tubo de aço tem seção transversal elíptica de dimensões médias mostradas na figura e espessura constante de . Se a tensão de cisalhamento admissível for , determine a dimensão b necessária para resistir ao torque mostrado. A área média para a elipse é
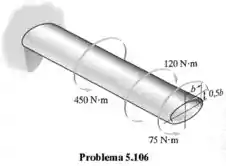
Passo 1
Vamos começar desenhando um diagrama de corpo livre e resolvendo a reação de apoio.
Como os únicos esforços são torções, a única reação de apoio será de torção.
Passo 2
Agora vamos analisar diferentes seções da barra para encontrar o ponto de maior torque
Observando as diferentes seções, observamos que o maior torque interno ocorre na Seção AB com o valor de
Passo 3
Agora, finalizamos a questão aplicando a Equação 5.18 e substituindo a área da elipse nela.
Resposta
Exercícios de Livros Relacionados
O tubo é feito de plástico, tem 5m m de espessura, e as dimensões médias mostradas na figura. Determine a tensão de cisalhamento média nos pontos A e B se ele for submetido ao torque T=5N ⋅ m . Mostre
Um tubo com as dimensões mostradas na figura é submetido a um torque a T= 50N ⋅ m . Desprezando as concentrações de tensão em seus cantos, determine a tensão de cisalhamento média no tubo nos pontos A
Determine a espessura constante do tubo retangular se a tensão de cisalhamento média não pode ultrapassar 84M P a quando um torque T = 2,5k N ⋅ m for aplicado ao tubo. Despreze as concentrações de ten
O tubo de aço inoxidável 304 tem espessura de 10m m . Se a tensão de cisalhamento admissível for τ a d m=80M P a , determine o torque máximo T que ele pode transmitir. Calcule também o ângulo de torçã
Dois eixo maciços de aço são acoplados pelos flanges em B e engastados a suportes rígidos em A e C. Para o torque mostrado, determinar a máxima tensão de cisalhamento (a) no eixo AB (b) no eixo BC.