Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 92
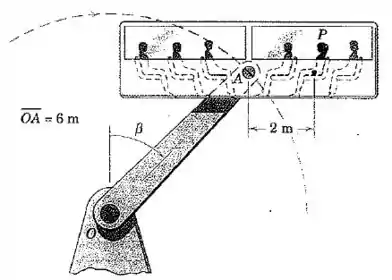
A atração de parque de diversões consiste em um suporte fixo junto a , do braço , que gira em torno do eixo em , e do compartimento, que permanece horizontal por meio de um mecanismo em (não apresentado). Em um determinado instante, , , e , todos no sentido horário. Determine as forças horizontal e vertical ( e ) exercidas pelo banco sobre o passageiro de em . Compare seus resultados com os valores estáticos destas forças. Note que todo passageiro se desloca em um círculo com um raio de .
Passo 1
Vamos começar lembrando de duas fórmulas importantes para essa questão. A componente tangencial da aceleração (em coordenadas polares) é:
Mas , então:
E a componente radial é:
Mas , então:
Então só o que precisamos fazer é determinar essas grandezas e as forças em cada uma dessas direções.
Passo 2
Então vamos desenhar um diagrama de forças sobre o passageiro no ponto . Esse passageiro não vai “orbitar” o mesmo centro que os outros, mas o raio da sua trajetória necessariamente é o mesmo.
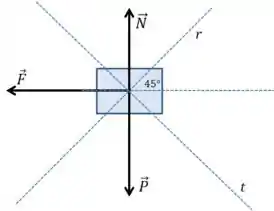
Onde é a força que o encosto faz sobre o passageiro, e é a força vinda do assento. Quais são as componentes das forças em cada direção?
E podemos resolver esse sistema para calcular as forças e .
Passo 3
Vamos reescrever o sistema (dividindo tudo por ):
lembrando que temos os seguintes valores pelo enunciado: ; ; ; . (O sinal negativo aparece porque os valores dados no enunciado estavam no sentido horário)
Somando as duas equações:
E subtraindo a primeira da segunda:
Passo 4
E agora só falta comparar com o caso estático. Nesse caso a única força em ação é o peso do passageiro, que precisa ser compensado pela força normal do assento:
Resposta
e , e no caso estático e .