Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.7 - Ex. 173
Os carros de uma atração de um parque de diversões têm uma velocidade na parte mais baixa do trilho. Determine sua velocidade na parte mais alta do trilho. Despreze as perdas de erergia devidas ao atrito. (Cuidado: Analise cuidadosamente a variação de energia potencial do conjunto de carros)
Passo 1
Vamos começar resolvendo tudo como se o conjunto de carros fosse uma única partícula concentrada na metade do comprimento do trem.
Vamos chamar os raios desenhados na figura de . Ainda olhando para a figura dá pra ver que o deslocamento total na vertical é:
Se considerarmos que a energia potencial gravitacional é nula no ponto onde a velocidade é podemos usar a conservação de energia para escrever o seguinte:
Passo 2
Ok, agora para aplicar isso ao caso em que o conjunto não está concentrado na metade do trem temos que calcular o do centro de massa.
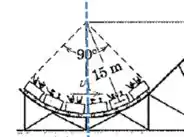
Como o trem já é simétrico em torno dessa linha pontilhada, sabemos que o centro de massa vai estar em algum lugar nessa linha, mas falta calcular a coordenada vertical dele.
E os limites ficaram entre e considerando que está sobre a linha pontilhada.
Pronto, e como já vimos que o centro de massa está sobre aquela linha pontilhada, podemos refazer a conta do passo com:
Passo 3
Retomando a fórmula de antes:
Vamos substituir o valor que encontramos:
E , então:
Resposta
A velocidade na parte mais alta do trilho é .