Substitua a corda do Prob. por uma corrente de elos com a mesma massa por unidade de comprimento. A extremidade livre recebe uma velocidade constante para cima . Escreva expressões para , para a tração na parte inferior da parte móvel, e para a força que suporta a extremidade fixa em termos de . Encontre também a perda de energia em termos de .
Figura do Prob. :
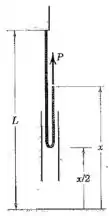
Passo 1
Vamos começar procurando uma expressão para a tração na parte inferior da parte móvel.
Bom, essa tração é uma reação ao fato de que a corrente está sendo puxada para cima, gerando um “escoamento” para o lado direito. Olhando para a figura podemos ver que a massa de corrente do lado direito é:
E então a taxa é:
E já qua a corrente adquite uma velocidade constante :
Passo 2
Agora vamos olhar par a parte direita da corrente (a que está em movimento), como a sua velocidade é constante, podemos garantir que a soma das força externas é nula:
E as forças que agem sobre essa parte da corrente são:
Passo 3
Beleza, já temos a força , agora vamos procurar . Vamos fazer algo parecido com o passo , mas aplicando ao lado esquerdo da corrente:
Onde é o comprimento da parte esquerda (fixa) da corrente.
É interessante ver que, ao contrário do que acontece no problema , em que tratamos de uma corda, a tensão sobre o lado esquerdo da corrente é nula.
Passo 4
Falta calcular a perda de energia em termos de . Vamos começar pensar um pouco na energia do sistema. A variação da energia cinética é:
Porque estamos considerando simplesmente a massa e a velocidade da parte móvel. Pela mesma lógica, a variação da energia potencial do sistema também se deve apenas à elevação dessa parte:
Como a única força produzindo deslocamento na direção da cordenada é , podemos considerar que o trabalho realizado sobre o sistema é:
E a diferença entre esse trabalho e a variação da energia mecânica é a perda de energia que estamos procurando:
Resposta
, , e .