Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 2.Problemas - Ex. 90
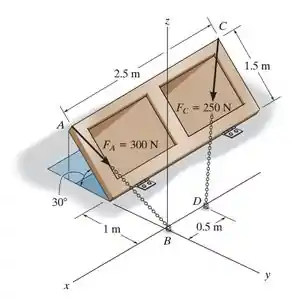
A porta é mantida aberta por duas correntes. Se as trações em e em são e , respectivamente, expresse cada uma dessas forças na forma de um vetor cartesiano.
Passo 1
Para expressar nossas forças como vetor vamos começar encontrando as coordenadas dos pontos que definem a sua direção:
Para
Para :
Temos então:
Definimos agora nossos vetores posição pelo ponto final menos inicial com seus devidos vetores unitários, assim:
Passo 2
Agora encontramos o módulo dos nossos vetores:
E então o vetor unitário que determina a direção e o sentido dos nossos vetores são:
Passo 3
Com isso, podemos expressar nossas forças como vetores cartesianos:
Resposta
Exercícios de Livros Relacionados
Se F possui uma intensidade de 250N , determine a intensidade de suas componentes projetadas que atuam ao longo do eixo x e do cabo A C .
Determine os componentes x , y e z da força F que atua no tetraedro como mostrado. Os valores de a , b e c e F são conhecidos e M é o ponto médio da aresta A B .
145- Um role de uma trena com 30m de comprimento tem uma massa de 0.283k g . Calcule a deflexão h na metade da fita quando ela é esticada entre dois pontos, situados no mesmo nível, por uma força trat
133. Dois cabos exercem forças sobre o tubo. Determine a intensidade da componente projetada de F 1 ao longo da linha de ação de F 2 .
137. Determine o ângulo θ entre os segmentos de tubo B A e B C .