Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.2 - Ex. 32

Um policial motociclista parte do repouso em dois segundos depois que um carro, correndo a uma velocidade constante de , passa pelo ponto . Se o patrulheiro acelera a uma taxa de até que atinja a sua velocidade máxima admissível de , que ele mantém, calcule a distância do ponto para o ponto em que ele ultrapassa o carro.

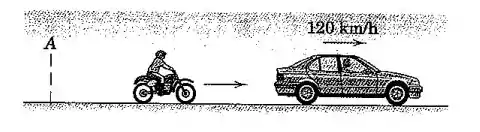
Passo 1

O primeiro passo é descobrir o quanto o policial anda enquanto ele acelera do repouso até sua velocidade de :

E quanto tempo ele demora para fazer isso?

Como o policial só começa a acelerar dois segundos depois que o carro passa (com sua velocidade ), o carro se desloca por até que o policial “termine de acelerar”:

Passo 2

Ok, então agora temos a seguinte situação:

E os dois estão se movendo com velocidade constante, então para saber o ponto onde eles se encontram é só usar essa equação:

E substituindo em qualquer uma das duas fórmulas:

Resposta

A distância é .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula move-se ao longo de uma trajetória de uma linha reta y = 0,5 x . Se a componente da velocidade da partícula é v x = ( 2 t 2 ) m/s, onde t é dado em segundos, determine a intensidade da v

Uma partícula está se movendo ao longo de uma trajetória reta. Se a sua posição ao longo do eixo x é x = ( 8 t ) m , onde t é dado em segundos, determine sua velocidade escalar quanto t =2 s .

Uma partícula é forçada a se mover ao longo da trajetória. Se x = ( 4 t 4 ) m, onde é dado em segundos, determine a intensidade da velocidade e da aceleração da partícula quanto t = 0,5 s.

12.82 Um carro desloca-se 2 km para leste por 5 minutos em seguida, 3 km para norte por 8 minutos em seguida, 4 km para oeste por 10 minutos. Determine a distância total percorrida e a intensidade do

39. Levando em consideração a variação da aceleração gravitacional a com relação à altitude y ( ve Problema 12.38), deduza uma equação que relacione a velocidade de uma partícula caindo livremente com