Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.2 - Ex. 26
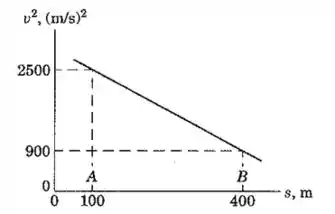
Um corpo se move em uma linha reta com uma velocidade cujo quadrado diminui linearmente com o deslocamento entre dois pontos e , que estão afastados como mostrado na figura. Determine o deslocamento do corpo durante os últimos segundos antes da chegada em .
Passo 1
Beleza, estamos lidando com duas grandezas: e . Qual equação a gente conhece que relaciona essas duas?
Certo, e se a gente definir que , então , e então:
Quais informações a gente pode tirar do gráfico? Bom, quando nós colocamos no eixo e no eixo essa equação vira uma reta:
Passo 2
Então vamos usar o gráfico para, primeiro, calcular a inclinação da reta:
E agora a gente pode calcular o valor de :
Beleza, agora falta calcular o deslocamento nos últimos dois segundos do movimento antes de chegar em .
Passo 3
Bom, para começo de conversa, em qual instante do tempo o corpo chega em ?
Olhando o gráfico:
Ótimo, então a gente já sabe que em o deslocamento do corpo é , vamos ver qual era o deslocamento dois segundos mais cedo :
E então o deslocamento nesse intervalo foi:
Pronto!
Resposta
O deslocamento nos últimos dois segundos é .