Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.2 - Ex. 22
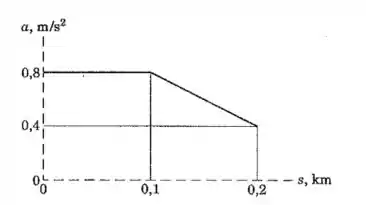
Um veículo entra em uma seção de teste de uma estrada reta em com uma velocidade de . Em seguida sofre uma aceleração que varia com o deslocamento como mostrado na figura. Determine a velocidade do veículo quando este passa pela posição .
Passo 1
O enunciado já diz que a velocidade inicial é , e pelo gráfico nós sabemos que o veículo se mantém com aceleração constante enquanto se desloca por .
Então, usando a equação de Torricelli:
Onde é a velocidade quando o deslocamento é .
Passo 2
Beleza, agora precisamos descobrir qual é a velocidade quando . Se concentre só no segundo trecho do gráfico!
Vamos usar a seguinte relação:
E podemos usar a regra da cadeia para escrever:
Mas , então:
E separando as variáveis:
Integrando os dois lados:
Passo 3
A integral da esquerda dá o seguinte resultado:
E como estamos analisando o intervalo entre e , a velocidade inicial é a que calculamos ali em cima:
E a integral da direita é simplesmente a área embaixo do gráfico nesse trecho (lembre de converter a distância para metros!):
E agora substituindo tudo na equação:
Resposta
A velocidade do veículo nessa posição é .