Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 77
O pequeno objeto é colocado sobre a superfície interna do prato cônico no raio mostrado. Se o coeficiente de atrito estático entre o objeto e a superfície cônica é , para qual faixa de velocidades angulares em torno do eixo vertical o bloco permanecerá sobre o prato sem deslizar? Assuma que as variações de velocidade são realizadas lentamente de modo que qualquer aceleração angular pode ser desprezada.
Passo 1
Primeiro vamos tentar entender o sentido físico do problema: se o prato gira rápido demais, a ação “centrífuga” vai fazer com que o objeto se mova para cima. Se o prato gira devagar demais, o peso do objeto vai fazê-lo deslizar para baixo.
Vamos começar procurando o valor mínimo da velocidade angular para que o bloco não deslize para baixo. Nesse caso, o atrito estático vai ser voltado para cima, pois ele se opõe ao deslizamento:
Na direçao da linha pontilhada , que contém o centro da trajetória circular, tem que existir uma resultante centrípeta, ou seja:
E na direção vertical a resultante tem que ser nula:
Passo 2
Agora vamos resolver esse par de equações, primeiro precisamos reescrever a força de atrito como:
E pela segunda equação temos:
Substituindo isso na primeira:
E então:
Esse é o valor mínimo da velocidade angular para que o bloco não escorregue para baixo.
Passo 3
Para encontrar o valor máximo, precisamos apenas fazer uma modificação simples: alterar o sentido da força de atrito.
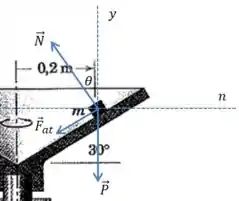
E não precisamos refazer a conta toda, é só trocar o sinal nos termos que envolvem o atrito na nossa fórmula final da velocidade angular mínima:
Trocando os sinais ficamos com:
E substituindo os mesmos valores numéricos:
E então o intervalo de velocidades em que o bloco não desliza é:
Resolvido!
Resposta
A velocidade angular precisa ficar entre e .