Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 120

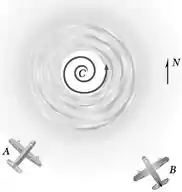
Os aviões A e B estão voando à mesma altitude e acompanhando o olho de um furacão C. A velocidade relativa de C em relação a A é vC/A = 235 km/h 40°. Determine (a) a velocidade relativa de B em relação a A, (b) a velocidade de A se um radar baseado no chão indica que o furacão está se movendo a uma velocidade escalar de 36 km/h para o norte, (c) a mudança na posição de C em relação a B durante um intervalo de 15 min.

Passo 1

  1. Nós temos

    2. v C = v A + v C / A

    e

    v C = v B + v C / B

    Então

    v A + v C / A = v B + v C / B

    ou

    v B - v A = v C / A - v C / B

    Agora

    v B - v A = v B / A

    de modo a

    v B / A = v C / A - v C / B

    ou

    v C / A = v C / B + v B / A

    A representação gráfica da última equação é então conforme mostrado.

    Nós temos

    v B / A 2 = 235 2 + 260 2 - 2 235 260 cos ⁡ 65 °

    v B / A = 266.798   mi/h

    260 sin ⁡ α = 266.798 sin ⁡ 65 °

    α = 62.03 °

    Passo 2

  2. Nós temos

    3. v C = v A + v C / A

    ou

    v A = 24   mi/h j - 235   mi/h - cos ⁡ 75 ° i - sin ⁡ 75 ° j

    v A = 60.822   mi/h i + 250.99   mi/h j

    Passo 3

  3. Notando que as velocidades de B e C são constantes. Nós temos

r B = r B 0 + v B t                 r C = r C 0 + v C t

Agora

r C / B = r C - r B = r C 0 - r B 0 + v C - v B t

= r C 0 - r B 0 + v C / B t

Então

∆ r C / B = r C / B t 2 - r C / B t 1 = v C / B t 2 - t 1 = v C / B ∆ t

Para ∆ t = 15 min:

∆ r C / B = 260   mi/h 1 4 h = 65   mi

Resposta

a )   v B / A = 258   mi/h     12.97 °

b )   v A = 258   mi/h     76.4 °

c )   ∆ r C / B = 65   mi     40 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A mola de 350m m é comprimida para um comprimento de 200m m , quando é liberada a partir do repouso e acelera o bloco deslizante A . A aceleração tem um valor inicial de 130m / s ² ² e em seguida dimi
Uma partícula se movendo ao longo do sentido positivo de x com uma velocidade inicial de 12m / s é submetida a uma força retardadora que lhe dá uma aceleração negativa a qual varia linearmente com o t
Para testar os efeitos de “ausência de peso” por curtos períodos de tempo, uma instalação de teste foi projetada para acelerar um volume de teste verticalmente para cima de A para B por meio de um pis
Um veículo entra em uma seção de teste de uma estrada reta em s = 0 com uma velocidade de 40k m / h . Em seguida sofre uma aceleração que varia com o deslocamento como mostrado na figura. Determine a
Um corpo se move em uma linha reta com uma velocidade cujo quadrado diminui linearmente com o deslocamento entre dois pontos A e B , que estão afastados 300m como mostrado na figura. Determine o deslo