Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.2 - Ex. 30
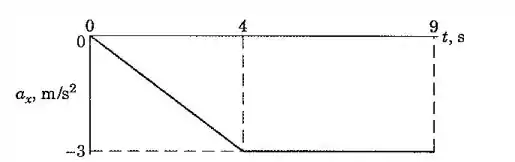
Uma partícula se movendo ao longo do sentido positivo de com uma velocidade inicial de é submetida a uma força retardadora que lhe dá uma aceleração negativa a qual varia linearmente com o tempo para os primeiros segundos como mostrado na figura. Para os próximos segundos a força é constante e a aceleração também permanece constante. Faça um gráfico da velocidade da partícula durante os segundos e especifique o seu valor em . Encontre também a distância percorrida pela partícula desde sua posição até o ponto em que esta inverte sua direção.
Passo 1
A primeira coisa a fazer é escrever uma equação para a aceleração em função do tempo. A ideia é fazer isso só olhando o gráfico.
Entre e , o gráfico é uma reta, e por isso tem uma equação desse tipo:
Como o gráfico cruza o eixo no ponto , sabemos que , e para calcular a inclinação é só fazer:
E então:
E entre e , é simplesmente uma função constante em , então temos:
Passo 2
Para encontrar a equação da posição em função do tempo precisamos integrar essa função duas vezes;
Fazendo isso na equação acima, vamos achar o seguinte:
Mas tome cuidado: , mas é a velocidade “inicial” do segundo trecho do gráfico, ou seja:
Além disso , mas :
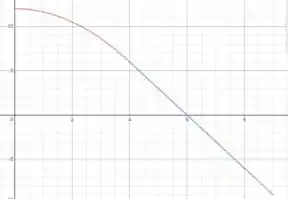
E assim já podemos fazer o gráfico:
Passo 3
E agora integrando mais uma vez para encontrar a posição:
Olhando o gráfico de cima, dá pra perceber que a partícula inverte sua posição quando . E usando a equação que encontramos para o podemos calcular que, nos primeiros quatro segundos:
E nos próximos dois segundos:
Ou seja, o deslocamento total é:
Resposta
A distância percorrida é .