Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.2 - Ex. 27
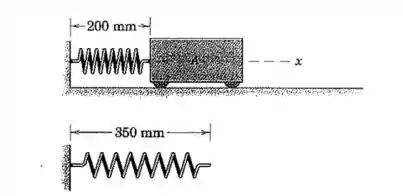
A mola de é comprimida para um comprimento de , quando é liberada a partir do repouso e acelera o bloco deslizante . A aceleração tem um valor inicial de e em seguida diminui linearmente com o movimento do bloco, chegando a zero quando a mola recupera o seu comprimento original de . Calcule o tempo para o bloco ir até (a) e (b) .
Passo 1
A aceleração do bloco vai seguir a seguinte expressão:
E como quando (o deslocamenteo a partir do ponto onde a mola é completamente achatada):
Então podemos escrever o seguinte:
Passo 2
Ok, como vamos aproveitar isso? Vamos lembrar da seguinte relação:
E integrando:
Passo 3
Precisamos transformar isso em uma função do tempo. Vamos lembrar da definição de velocidade:
Essa é uma integral do tipo:
Bom pessoal, essa não é uma integral simples de resolver, a melhor opção é consultar uma tabela ou resolver numericamente.
Resolvendo numericamente, para , temos:
E para , temos:
Resposta
(a)
(b)