Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 123
Sabendo que no instante mostrado na figura o bloco A tem velocidade de 8 cm/s e aceleração de 6 cm/s² , ambas no sentido de descida da rampa, determine (a) a velocidade do bloco B, (b) a aceleração do bloco B.
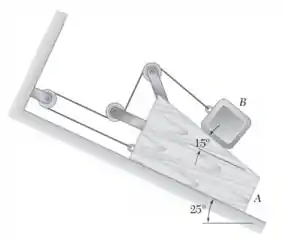
Passo 1
Do diagrama a seguir podemos começar a determinar o que o exercício pede :D
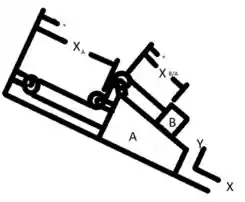
Então
Note que edevem ser paralelos ao topo da superficie do bloco A.
Passo 2
(a)Nós temos
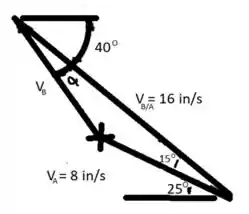
A representação gráfica dessa equação é a mostrada. Note que por causa de A se mover para baixo, B deve se mover para cima relativamente a A.
ou
e
ou
Passo 3
(b)A mesma técnica que foi usada para determinar pode ser usada para determinar. Um metodo alternativo segue.
Nós temos
*
)i+(3.1058i m/s²)j
ou
*Note que a orientação dos eixos das coordenadas no sistema desenhado.
Resposta
Exercícios de Livros Relacionados
Um corpo que se move em uma linha reta entre dois pontos A e B afastados de uma distância de 50m tem uma velocidade cujo quadrado aumenta linearmente com a distância percorrida, como mostra o gráfico.
Um determinado lago é proposto como uma área de aterrissagem para grandes aviões a jato. A velocidade de aterrissagem de 160k m / h no contato com a água deve ser reduzida para 30k m / h em uma distân
Calcule a velocidade de impacto de um corpo liberado a partir do repouso a uma altitude h = 800k m . (a) suponha uma aceleração gravitacional constante g 0 = 9,81m / s ² ² e (b) considere a variação d
Calcule a velocidade de impacto de um corpo A que é liberado a partir do repouso a uma altitude h = 1200k m acima da superfície da lua. (a) suponha inicialmente uma aceleração gravitacional constante
Uma partícula se movendo ao longo de uma linha reta desacelera de acordo com a = - k v , onde k é uma constante e v é a velocidade. Se a sua velocidade inicial no instante t = 0 , é v 0 = 4m / s e a s