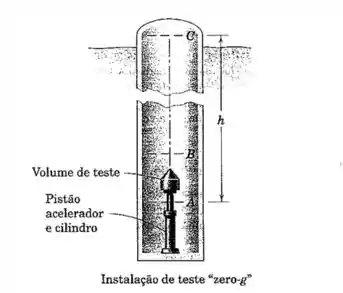
Para testar os efeitos de “ausência de peso” por curtos períodos de tempo, uma instalação de teste foi projetada para acelerar um volume de teste verticalmente para cima de para por meio de um pistão acionado a gás e que permite subir e descer de para para sob condições de queda livre. A câmara de ensaio consiste em um poço profundo que é evacuado para eliminar qualquer resistência apreciável do ar. Se uma aceleração constante de de para é fornecida pelo pistão e se o tempo total de teste para a condição de “ausência de peso” de para para é de , calcule a altura de trabalho requerida pela câmara. Retornando para , o volume de teste é recuperado em uma cesta cheia com aglomerados de poliestireno inserida na linha de queda.

Nosso objetivo é calcular a altura da instalação de teste. Primeiro vamos tentar calcular o comprimento do trajeto .

O que a gente já sabe? Que o volume começa com uma velocidade de e é “freado” pela gravidade até parar. Usando a equação de Torricelli:

E esse vai ser justamente o comprimento do trajeto !

Falta achar o comprimento do trajeto .

O que a gente sabe sobre esse trajeto?

O enunciado disse que a aceleração nesse intervalo é , e nós sabemos que o volume vai de até , então vamos usar a mesma equação:

E dessa vez o é o comprimento do trajeto :

E agora somando tudo temos:

Resolvido!