Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.9 - Ex. 188
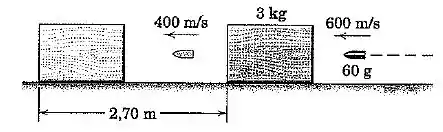
Uma bala de é disparada horizontalmente com uma velocidade contra o bloco de de madeira macia inicialmente em repouso sobre a superfície horizontal. A bala emerge do bloco com a velocidade , e se observa que o bloco desliza uma distância de antes de parar. Determine o coeficiente de atrito dinâmico entre o bloco e a superfície de apoio.
Passo 1
O primeiro passo é descobrir quanta energia a bala consegue passar para o bloco de . Pela lei de conservação do momento linear, podemos afirmar o seguinte:
Isso quer dizer que a energia com que o bloco começa a se mover é:
Passo 2
Então tá, mas como vamos calcular o coeficiente de atrito a partir disso? Bom, se o bloco vai parar após andar , quer dizer que alguém realizou trabalho sobre ele, ou seja:
Só precisamos calcular qual é o valor de para que esse seja o trabalho realizado após .
Como o bloco está andando no plano, a força normal é igual à força peso:
E o trabalho realizado por essa força é:
Passo 3
Agora vamos resolver essa última equação:
E como o próprio enunciado já disse, o deslocamento total é :
Resposta
O coeficiente de atrito deve ser .