Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 57
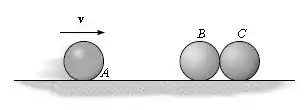
Cada uma de três bolas tem uma massa . Se tem uma velocidade imediatamente antes da colisão direta com , determine a velocidade de após a colisão. O coeficiente de restituição entre cada bola é . Despreze a dimensão de cada bola.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Aplicando conservação de quantidade de movimento, temos:
Substituindo os valores, temos:
O coeficiente de restituição é dado por:
Substituindo os valores, temos:
Resolvendo o sistema, temos:
Quando a bola atinge , temos:
O coeficiente de restituição é dado por:
Substituindo os valores, temos:
Resolvendo o sistema, temos:
Resposta
Exercícios de Livros Relacionados
Um painel deslizante de 40 kg é suportado pelos roletes em B e C. Um contrapeso A de 25 kg é fixado por cabo como mostrado na figura e, nos casos a e c, estão em contato com a borda vertical do painel
Um carro está viajando em uma estrada com inclinação lateral a uma velocidade constante v. Determine o intervalo de valores de v para os quais o carro não derrapa. Expresse sua resposta em termos do r
Um caixote B de 500 kg está suspenso por um cabo preso a um carrinho A de 40 kg que corre por uma viga I inclinada, tal como mostra a figura. Sabendo que no instante mostrado o carrinho tem uma aceler
Um fio único ACB de 80 cm de comprimento passa por um anel em C que está preso a uma esfera que roda com uma velocidade escalar constante v no círculo horizontal mostrado na figura. Sabendo que θ 1 =
Um caixote B de 500 kg está suspenso por um cabo preso a um carrinho A de 40 kg que corre por uma viga I inclinada, tal como mostra a figura. Sabendo que no instante mostrado o carrinho tem uma aceler