Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 32

A bala de canhão de 5   k g é disparada horizontalmente por um canhão de 250   k g , como mostra a figura. Se a velocidade de saída da bala é 600   m / s , medida relativamente ao solo, determine a velocidade de recuo do canhão logo após o disparo. Se o canhão está em repouso sobre um apoio liso e será parado depois de haver recuado por uma distância de 150   m m , determine a rigidez necessária k das duas molas idênticas, cada uma das quais está originariamente não estendidas.

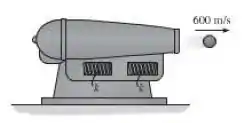
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Podemos aplicar conservação de quantidade de movimento para encontrar a velocidade de recuo do canhão:

→ +         m c v c 1 + m b v b 1 = m c v c 2 + m b v b 2

Substituindo os valores, temos:

→ +         250 0 + 5 0 = 250 v c 2 + 5 600

v c 2 = - 12   m / s

v c 2 = 12   m / s   ( ← )

Passo 2

Agora que sabemos a velocidade de recuo, podemos aplicar o princípio da conservação de energia para encontrar a rigidez k das molas. Lembrando que o sistema é composto por duas molas.

T 1 + V 1 = T 2 + V 2

1 2 m c v c i + 1 2 2 k s i 2 = 1 2 m c v c f + 1 2 2 k s f 2

Substituindo os valores, temos:

1 2 250 12 2 + 1 2 2 k 0 2 = 1 2 250 0 + 1 2 2 k 0,15 2

2 k 0,15 2 = 250 12 2

k = 800   k N / m

Resposta

k = 800   k N / m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

140. Determine a intensidade da força F como uma função do tempo, que dever ser aplicada à extremidade da corda em A para levantar o gancho H com uma velocidade constante v = 0,4 m s . Inicialmente, a
137. Um rolo de corrente aberta e pesada é usada para reduzir a distancia de parada de um trenó, que tem massa M e viaja a uma velocidade v 0 . Determine a massa por unidade de comprimento da corrente
19. Um bloco de 15Kg move-se inicialmente por uma superfície horizontal lisa, com uma velocidade escalar v 1 = 1,8 m s para esquerda. Se sobre ele age uma forca F, que varia do modo mostrado, determin
20. Determine a velocidade de cada bloco 2 segundos depois de serem liberados do repouso. Despreze a massa das polias e da corda.
Uma linha de n esferas similares, cada uma com massa m , estão colocadas próximas uma a outra, como mostrado. Se a esfera 1 tem uma velocidade v 1 , determine a velocidade da n - 1 -ésima. O coeficien