Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 73

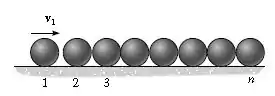
Uma linha de n esferas similares, cada uma com massa m , estão colocadas próximas uma a outra, como mostrado. Se a esfera 1 tem uma velocidade v 1 , determine a velocidade da n - 1 -ésima. O coeficiente de restituição entre esferas é e .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Bom, pra resolver essa questão, vamos aplicar a conservação de movimento linear algumas vezes e ver como é o comportamento e definir a velocidade da n - 1 -ésima esfera.

Vamos definir os momentos antes e depois do impacto:

→ +       ∑ m v 1 = ∑ m v 2

m v 1 + 0 = m v 1 ' + m v 2 '

v 1 ' + v 2 ' = v 1

Precisamos de outra equação para resolver o sistema, temos:

→ +       e = v 2 ' - v 1 ' v 1 - 0

v 2 ' - v 1 ' = e v 1

Relacionando as equações e resolvendo o sistema, temos:

v 2 ' = 1 + e 2 v 1

Passo 2

Agora vamos fazer o mesmo procedimento novamente entre as esferas 2 e 3 . Temos:

m 1 + e 2 v 1 + 0 = m v 2 ' ' + m v 3 '

v 2 ' ' + v 3 ' = 1 + e 2 v 1

Precisamos de outra equação para resolver o sistema, temos:

→ +       e = v 3 ' - v 2 ' ' 1 + e 2 v 1 - 0

v 3 ' - v 2 ' ' = e 1 + e 2 v 1

Relacionando as equações e resolvendo o sistema, temos:

v 3 ' = 1 + e 2 2 v 1

Passo 3

Se continuarmos com o mesmo procedimento encontraremos:

v 4 ' = 1 + e 2 3 v 1

Podemos então definir a velocidade da n -ésima esfera como:

v n ' = 1 + e 2 n - 1 v 1

A velocidade da n - 1 -ésima esfera será:

v n - 1 ' = 1 + e 2 n - 2 v 1

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O motor de foguete de uma nave espacial com 30t se deslocando a uma velocidade de 24000k m / h é acionado e produz um empuxo de 20k N na direção de sua trajetória circular durante um período de 3m i n
O avião de caça tem uma massa de 6450k g e precisa de 10 segundos a partir do repouso para atingir a sua velocidade de decolagem de 250k m / h sob o empuxo constante do jato T = 48k N . Calcule a médi
Se a resistência R ao movimento de um trem de carga de massa total m aumenta com a velocidade de acordo com R = R 0 + K v , onde R 0 é a resistência inicial a ser superada na partida do trem e K é uma
Uma nave espacial com uma massa de 260k g está se deslocando com uma velocidade u = 30000k m / h na direção fixa x afastada de qualquer corpo celeste que a possa atrair. A nave espacial é estabilizada
A bola de golfe com 45,9g é batida pelo taco de ferro número cinco e adquire a velocidade mostrada em um período de tempo de 0,001s . Determine o módulo R da força média exercida pelo taco sobre a bol