Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 137

137. Um rolo de corrente aberta e pesada é usada para reduzir a distancia de parada de um trenó, que tem massa M e viaja a uma velocidade v 0 . Determine a massa por unidade de comprimento da corrente, necessária para desacelerar o trenó até 1 2 v 0 , dentro de uma distancia de x = s , se o trenó está preso a corrente em x = 0 . Despreze o atrito entre a corrente e o solo.

Passo 1

Neste tipo de problema seria importante fazer um esboço da situação que o enunciado descreve para sabermos quais são as forças que estão envolvidas no problema e a partir daí utilizar as equações desenvolvidas ao longo da seção para problemas que envolvem foguetes.

Passo 2

Um esboço do que está sendo dito no enunciado pode ser representado por:

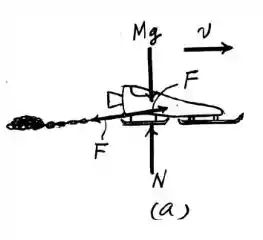
Passo 3

Da equação 15.28, temos que:

∑ F s = m . d v d t - v D e . d m e d t

0 = m ´ x + M d v d t + v m ´ v

0 = m ´ x + M d v d t + m ´ v 2

Como sabemos que v = d x d t podemos escrever que d t = d x v . Substituindo na equação acima teremos:

0 = m ´ x + M v d v d x + m ´ v 2

m ´ x + M v d v d x = - m ´ v 2

d v d x = - m ´ v m ´ x + M

d v v = - m ´ m ´ x + M d x

Integrando a expressão acima utilizando as informações de que quando v = v 0 x = 0 e v = 1 2 v 0 x = s , teremos:

∫ v 0 1 2 v 0 d v v = - ∫ 0 s m ´ m ´ x + M d x

ln ⁡ v v 0 1 2 v 0 = - ln ⁡ ( m ´ x + M ) 0 s

1 2 = M m ´ s + M

m ´ = M s

Resposta

m ´ = M s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a velocidade escalar teórica máxima que um automóvel partindo do repouso pode atingir após ter percorrido 400 m. Assuma que o coeficiente de atrito estático é de 0,80 entre os pneus e o pavi
Os dois blocos mostrados na figura estão originalmente em repouso. Desprezando as massas das roldanas e o efeito do atrito nessas roldanas e considerando que os coeficientes de atrito entre ambos o bl
O bloco A tem a massa de 40 kg e o bloco B tem a massa de 8 kg. Os coeficientes de atrito entre todas as superfícies de contato são μ s = 0,20 e μ k = 0,15. Se P = 0, determine (a) a aceleração do blo
Duas esferas idênticas A e B, cada uma com massa m, estão conectadas por uma corda inextensível e não elástica de comprimento L, e em repouso a uma distância a uma da outra sobre uma superfície horizo
Em um cruzamento, o carro B ia para o sul e o carro A viajava 30° para nordeste, quando se envolveram em uma colisão. Pela investigação, soube-se que, após a batida, os dois carros se engataram e derr