Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 132
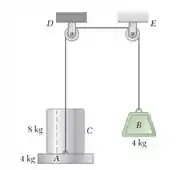
Um cilindro C de 8 kg repousa sobre uma plataforma A de 4 kg sustentada por uma corda que passa sobre as roldanas D e E e é presa a um bloco B de 4 kg. Sabendo que o sistema é liberado do repouso, determine (a) a velocidade do bloco B após 0,8 s, (b) a força exercida pelo cilindro sobre a plataforma.
Passo 1
Questões envolvendo sistemas de roldanas assustam um pouco, mas não é o Thanos. Para resolver vamos começar com o diagrama de corpo livre, representando a quantidade de movimento linear e o impulso provocado pelas forças envolvidas. Para o conjunto formado por A e C, e temos:
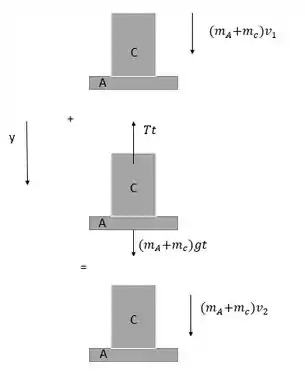
Como o movimento de A e C é para baixo, vamos definir esse sentido como positivo. Para B, o sentido positivo será para cima. Podemos observar que o peso de A e C provoca o movimento do conjunto de roldanas e que a força de tração da corda influencia no movimento. A equação que utilizaremos é o princípio de impulso e quantidade de movimento linear.
Passo 2
Para A e C temos:
Para B temos:
Somando as duas equações resultantes temos:
A velocidade final do bloco B após 0,8s será de 3,92 m/s.
Passo 3
Para a gente descobrir a força do cilindro, vamos o diagrama de corpo livre semelhante ao passo 1 somente para o bloco A:
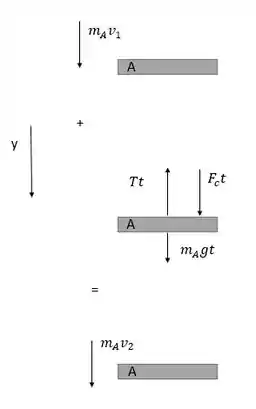
Aqui é a força que o cilindro exerce sobre o bloco A. Usando o princípio de impulso e quantidade de movimento linear temos:
Da equação para o bloco B, determinamos a força de tração da corda:
Com isso, podemos saber a força do cilindro:
Resposta
- 3,92 m/s
- -0,3 N