Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 119
Um automóvel de está movendo a uma velocidade quando os freios são totalmente aplicados, causando o escorregamento de todas as quatro rodas. Determine o tempo necessário para parar o automóvel no pavimento seco , na rodovia gelada .
Passo 1
Fala aí, galera. Tudo certo? Bora fazer mais um exercício de Dinâmica. Neste problema temos que calcular o tempo necessário para um automóvel parar, ou seja, em duas situações.
Na primeira, em pavimento seco, vamos aplicar o princípio de impulso e quantidade de movimento, dado por:
Em seguida, vamos esboçar um DCL para visualizarmos o que acontece no problema:
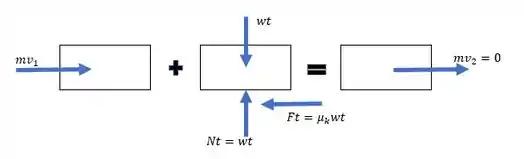
Com todas as forças representadas, podemos substituir na equação que relaciona o impulso e a quantidade de movimento. Como a velocidade final do carro é , temos:
Como cada força é constante em intensidade, direção e sentido, cada impulso correspondente é igual ao produto da força e do intervalo de tempo . Fica assim:
Opa, agora basta substituirmos os valores que o enunciado nos forneceu nesta equação. Para o asfalto seco, temos que , portanto:
Passo 2
Agora que encontramos a equação, fica mais fácil encontrar o tempo de parada no pavimento gelado. Para isso, basta utilizarmos a mesma equação, utilizando agora , logo:
É isso, galerinha. Bora praticar mais!