Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 135

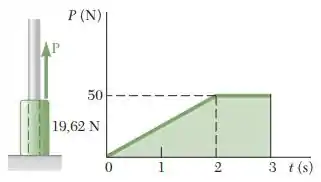
Um colar de 2 kg pode deslizar sobre uma barra vertical sem atrito e está sujeito a uma força P cuja intensidade varia como mostrado na figura. Sabendo que o colar está inicialmente em repouso, determine (a) a máxima velocidade do colar, (b) o tempo em que a velocidade é zero.

Passo 1

Essa questão dá um trabalhinho, mas não é tão difícil. Nesse caso vamos trabalhar com uma força que está em função do tempo, aplicando o princípio do impulso. Pelo gráfico, podemos ver que a força varia linearmente com o tempo de 0 a 2s, e depois torna-se constante. De t = 0s para t = 2s, força P é descrita como:

P t = 50 2 t = 25 t

Para 2,0 s

P t = 50   N

E para t > 3s

P t = 0

E o colar sai do repouso quando:

P t = W → 19,62 = 25 t → t = 0,78   s

Passo 2

A velocidade máxima a ser atingida pelo colar será no instante que o impulso for máximo. Observando o gráfico P(N) x t(s),

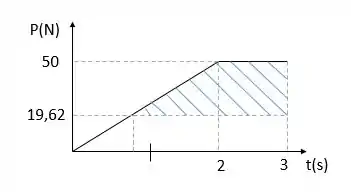
Temos que o máximo impulso será igual à área da região hachurada. Assim, temos:

I m p m á x = Á r e a = 1 + 3 - 0,78 ( 50 - 19,62 ) 2 = 48,91   N ⋅ s

Logo a velocidade máxima é calculada utilizando o princípio do impulso

m v 1 + I m p m á x = m v 2

0 + 48,91 = 2 v 2

v 2 = 24,4   m / s

Passo 3

Para calcular o instante que a velocidade é zero, ou seja, o instante após t = 3s que o colar irá ter velocidade final igual a zero. Como depois de 3 s a única força que age sobre o colar é o peso do próprio colar, temos que o princípio do impulso será descrito como

m v 2 - W Δ t = m v 3

Onde Δ t é o intervalo de tempo para a velocidade chegar a zero. Assim,

2 ⋅ 24,4 - 19,62 Δ t = 0

Δ t = 2,5   s

Logo, o instante de tempo final será

t = 3,0 + 2,5 = 5,5   s

Resposta

  1. 24,4 m/s
  2. 5,5 s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O caminhão de 5M g e o carro de 2M g estão viajando nas velocidades mostradas imediatamente antes de colidirem. Após a colisão o carro move-se com uma velocidade de 15k m / h para a direita em relação
A bola de 2k g é lançada de modo a se mover horizontalmente a 10m / s quando atinge o bloco de 6k g , que está descendo o plano inclinado a 1m / s . Se o coeficiente de restituição entre a bola e o bl
A bola de 2k g é lançada de modo a se mover horizontalmente a 10m / s quando atinge o bloco de 6k g , que está descendo o plano inclinado a 1m / s . Se o coeficiente de restituição entre a bola e o bl
Dois carros A e B têm massa de 2000k g e colidem no pavimento escorregadio de um cruzamento. A direção do movimento de carro após a colisão é medida pelos rastros deixados, como mostrado. Se o motoris
A bola de bilhar A move-se com uma velocidade de 10m / s imediatamente antes de atingir a bola B , que está em repouso. Se as massas de A e B são 200g cada e o coeficiente de restituição entre elas é