Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 3.Problemas - Ex. 33
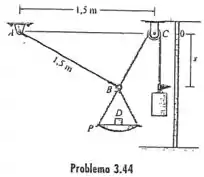
Uma balança é construída usando a massa de , o prato de e a montagem da polia e da corda conforme figura. A corda tem de comprimento. Se , determine a massa de no prato. Despreze a dimensão da polia.
Passo 1
Falaa, querido!
Para determinar a massa de D, deve-se fazer o equilíbrio de forças no sistema. Assim, o diagrama de corpo livre deve ser analisado, aplicando as equações de equilíbrio ao longo dos eixos.
Tem-se que a massa pendurada pela corda na extremidade direita exerce uma força peso de
Ao final, sabe-se que o prato juntamente com a massa D exercem uma força que vale:
A gente quer saber quanto vale . Bora!
Passo 2
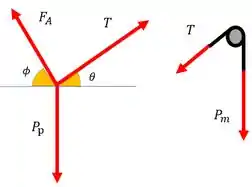
Perce que é a força no cabo que suporta o peso da massa de . Pelo equilíbrio, a tensão nas duas extremidades desse cabo devem ser iguais, logo
Aí a gente pode achar pelo equilíbrio de forças no ponto B.
Passo 3
Mas calma, a gente vai precisar decompor essas forças inclinadas nos eixos coordenados. Para isso precisamos descobrir os valores dos ângulos que elas fazem com a horizontal.
O segmento é a hipotenusa de um triângulo que contém . Podemos esboça-lo assim:
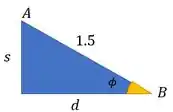
Aí a gente pode acha seu valor por trigonometria. Lembrando que .
Vamos achar também porque vai ajudar no outro ângulo:
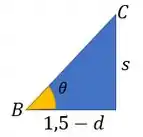
Aí a gente pode olhar para o triângulo retângulo que contém BC e :
Passo 4
O equilíbrio requer quer que o somatório de forças em cada dimensão seja nulo, ou seja:
Adotando o sentido dos eixos mostrado no desenho do enunciado:
Passo 5
Por fim, com os ângulos determinados e as equações (1) e (2), consegue-se obter:
E:
Portanto,