Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas Fundamentais - Ex. 27
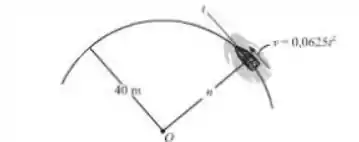
Um barco está se movendo ao longo da trajetória circular com uma velocidade escalar de , onde é dado em segundos. Determine a intensidade da sua aceleração quando .
Passo 1
Estamos começando por uma questão bem simples! Precisamos determinar a intensidade da aceleração após a passagem de 10 segundos. Para isto, precisamos determinar qual o valor das componentes normal e tangencial da aceleração. Para determinar a componente tangencial, basta lembrarmos que:
Já a componente normal, precisamos obter inicialmente o valor da velocidade no tempo, e em seguida, basta fazer:
Pronto! Temos todos os parâmetros necessários para obtermos a aceleração!
Passo 2
Vamos começar determinando a aceleração tangencial. Portanto, vamos derivar a velocidade em função do tempo. Sendo assim,
Quando , teremos:
Pronto, obtemos a componente tangencial da aceleração!
Passo 3
Precisamos determinar a componente tangencial da aceleração. Mas para isto, precisamos obter antes a velocidade do barco após a passagem do tempo. Substituindo o valor de , temos:
Substituindo este valor na equação da aceleração normal, temos:
Passo 4
Agora, só nos basta calcularmos a intensidade da aceleração. Sendo assim,