Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas Fundamentais - Ex. 31

Se a motocicleta tem uma desaceleração de a t = - 0,001 s   m / s 2 e sua velocidade escalar na posição A é 25   m / s , determine a intensidade da sua aceleração quando ela passa o ponto B.

Passo 1

Precisamos determinar o valor da aceleração no ponto B. Sendo assim, precisamos determinar suas componentes tangencial e normal! A sua componente tangencial já foi dada em função da posição. Precisamos então encontrar uma função para a normal, e para isto, vamos ter de determinar a velocidade da motocicleta no ponto B através das equações da cinética.

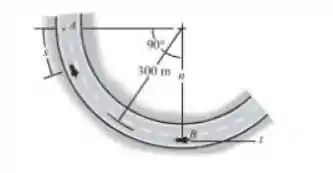
Este é o procedimento que temos de fazer. Entretanto, no final, fica um questionamento. Aonde está o ponto B? Qual a distância necessária para chega-lo nele? Este é o nosso ponto de partida!

Passo 2

Precisamos determinar inicialmente a distância percorrida para chegar ao ponto B, isto é, s B . Esta distância é bem simples de ser calculada. Basta perceber que a curva consiste em um arco de circunferência. E, para chegar a B, tem de ser percorrido a distância de π / 2 . Sim! Cuidado que o ângulo tem que estar escrito em radianos!!!

Sendo assim, a distância é:

s B = ρ ⋅ θ = 300 ⋅ π 2 = 471,2   m

Passo 3

Antes de calcularmos as componentes da aceleração, precisamos determinar a velocidade da moto. Para isto, temos de resolver a seguinte integral:

∫ v A v B v d v = ∫ s A s B a d s

Sabendo que s A = 0   m , s B = 471,2   m , v A = 25   m / s , temos então:

∫ 25 v B v d v = ∫ 0 471,25 - 0,001   s   d s

v B 2 - 25 2 2 = - 55,51 2

v B = 20,1   m / s

Passo 4

Agora, vamos calcular as componentes da aceleração. Começando pela componente tangencial, temos:

a t = - 0,001 ⋅ 471,2 = - 0,47   m / s 2  

Agora, calculando a componente normal,

a n = v 2 ρ = 20,1 2 300 = 1,34   m / s 2

Portanto, a intensidade da aceleração é dada por:

a = a n 2 + a t 2

a = 1,34 2 + ( - 0,47 ) 2

a = 1,42   m / s 2

Resposta

a = 1,42   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para um determinado intervalo de movimento o pino A é forçado a se deslocar na ranhura fixa parabólica pelo braço horizontal com encaixe que é elevado na direção y a uma taxa constante de 30m m / s .
A partícula P se desloca ao longo da ranhura curva, uma parte desta é mostrada. Sua distância em metros medida ao longo da ranhura é dada por s = t 2 / 4 , onde t é em segundos. A partícula está em A
Uma partícula que se move em um movimento curvilíneo tem coordenadas em milímetros que variam com o tempo t em segundos de acordo com x = 3 t 2 - 4 t e y = 4 t 2 - 1 3 t 3 . Determine os módulos da ve
Com que velocidade horizontal mínima u um menino pode jogar uma pedra em A e fazê-la por pouco ultrapassar a obstrução em B ?
Se o cano da espingarda mostrada aponta para o ponto A , calcule a distância δ abaixo de A até o ponto B onde a bala incide. A velocidade de saída no disparo da bala é de 600m / s .