Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 8.Problemas - Ex. 92
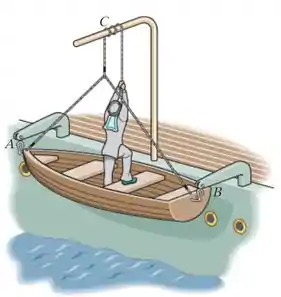
O barco tem um peso de e é mantido na posição lateral de um navio pelas vergas em e . Um homem com um peso de entra no barco, enrola uma corda em torno de uma lança em e a prende na extremidade do barco, conforme mostra a figura. Se o barco for desconectado das vergas, determine o número mínimo de meias voltas que a a corda precisa fazer em torno do mastro de modo que o barco possa ser abaixado com segurança para a água em velocidade constante. Além disso, qual é a força normal entre o barco e o homem? O coeficiente de atrito entre a corda e o mastro é . Dica: O problema exige que a força normal entre os pés do homem e o barco seja a menor possível.
Passo 1
Galera, essa questão foi bem legal com a gente porque já até nos deu uma dica! Vamos considerar que a força normal entre os pés do homem e o barco é igual a zero, beleza? Seja e . Então, aplicando a equação para o atrito entre corda e roldana, temos:
Aplicando o logaritmo natural dos dois lados da equação:
Assim, o menor número de meias voltas que a corda precisa é:
Para efeitos de resposta, vamos usar
Passo 2
Vamos agora encontrar a força normal entre o homem e o barco. Para um sistema em equilíbrio, o somatório de forças em e tem que ser igual a zero.
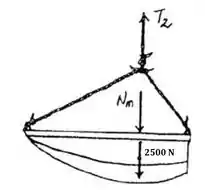
Assumindo que a direção para cima é positiva, temos para o eixo
Passo 3
Vamos olhar agora para a situação do homem. As forças que estão atuando em cima do homem são:
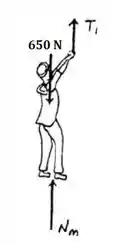
Para um sistema em equilíbrio, o somatório de forças em e tem que ser igual a zero. Assim, adotando como referencial positivo a direção para cima como positiva, temos:
Passo 4
Temos em mãos a tração na corda amarrada ao barco e a tração na mão do homem. O jeito que podemos usar para relacionar as duas é através da equação do atrito entre cordas e uma superfície de contato. Assim:
Resposta
O número mínimo de meias voltas é:
A força normal entre o barco e o homem é: