Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 116
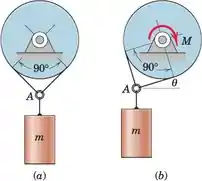
O cilindro de massa m é preso ao anel A, que fica suspenso pelo cabo que passa sobre a polia, conforme mostrado na parte a da figura. Um par M aplicado na polia gira-a até que o deslize do cabo na polia ocorra na posição , mostrado na parte b da figura. Calcule o coeficiente de atrito m entre o cabo e a polia.
Passo 1
O enunciado pede que a gente calcule o coeficiente de atrito m entre o cabo e a polia.
Passo 2
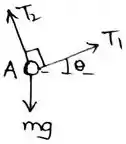
Para equilíbrio em A!
Para
Resposta
Exercícios de Livros Relacionados
O bloco e o equipamento mostrados são usados para elevar uma carga de 150 lb. Cada uma das polias de 3 pol. De diâmetro gira em um eixo de 0,5 pol. Sabendo que o coeficiente de atrito estático é 0,20,
Em Prob. 8.67, determine o par que deve ser aplicado ao eixo AB para girar a engrenagem grande no sentido horário.
Determine se o bloco mostrado está em equilíbrio e encontre a magnitude e a direção da força de atrito quando θ = 35° e P = 2 00N .
Determine se o bloco mostrado está em equilíbrio e encontre a magnitude e a direção da força de atrito quando θ = 30° e P = 30l b .
Uma alavanca A B de peso desprezível é montada com folga em um eixo fixo de 63m m de diâmetro. Sabendo que o coeficiente de atrito estático entre o eixo fixo e a alavanca é 0,15 , determine a força P