Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 92
O membro cilíndrico , vazado e de paredes finas, tem uma seção transversal não-circular e espessura não uniforme. Usando a expressão dada na Eq. (3.53), da Sec. 3.13, e a expressão para densidade de energia de deformação dada na Eq. (10.19), da Sec. 10.15, mostrar que o ângulo de torção do membro é:
onde é um elemento da linha média da espessura da seção transversal e é a área limitada por essa linha média.
Passo 1
E aí, meus queridos e minhas queridas! Aproveitando a vida? Então vamos aproveitar mais ainda, resolvendo essa questão de cálculo de ângulo de torção através do método da energia!
A questão quer que a gente calcule o ângulo de torção de uma barra submetida a um torque , usando o método da energia. Logo, usaremos uma equação que relaciona a energia absorvida pela a barra em torção com esse ângulo de torção pra achar .
é a energia total absorvida pela barra . No entanto, a questão pede que a gente calcule através da densidade de energia de deformação . Isso quer dizer que precisamos escrever em função de através da integral abaixo.
Além disso, a questão pede que a gente use a equação abaixo para encontrar em função da tensão de cisalhamento gerada pela torção. Por fim, o enunciado informa que, para calcular temos que usar a equação abaixo.
onde é a espessura variável do perfil da barra.
Com todas essas informações em mãos, vamos começar a resolver a questão.
Passo 2
Primeiro, devemos substituir a integral de na equação de que deduzimos.
Agora, substituímos por sua equação em função de .
A terceira etapa é substituir pela sua fórmula mostrada no passo 1.
Podemos colocar as constantes pra fora da integral. Mas cuidado! Lembre-se que a espessura varia ao longo do volume. Logo, não pode ser tirado da integral!
A questão pedir pra gente mostrar o valor de em função de uma integral em . No entanto, ao fazer todas essas substituições, só conseguimos chegar em uma equação com uma integral em . Por isso, no próximo passo, veremos como transformar a integral com em uma com .
Passo 3
Para transformar a integral com em uma integral com , precisamos descobrir quanto vale em função de . é uma pequena parte do volume da barra . Podemos ver na figura abaixo.
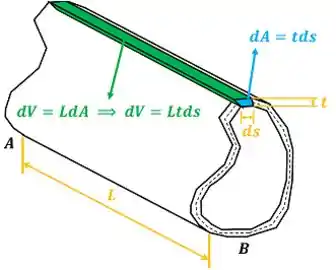
Antes de substituir o valor de presente na figura na integral que temos, precisamos lembrar de um fato. Quando mudamos a integral de pra integral de , devemos mudar o tipo de integral. A integral em passa a ser uma integral cíclica porque é uma pequena parte de uma curva fechada (um ciclo sem início nem fim). Levando isso em conta:
Aeeeee! Finalmente chegamos na equação que a questão pedia para a gente demonstrar! Isso é tudo, pessoal!
Resposta
Ei, a resposta está no passo a passo :)