Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.6 - Ex. 135

A barra AB do Prob. 5/72 é reapresentada aqui. Se a velocidade do ponto A é de 3 m/s para a direita e é constante para um intervalo incluindo a posição mostrada, determine a aceleração tangencial do ponto B ao longo de sua trajetória e a aceleração angular da barra.

Passo 1

Primeiramente, vamos buscar no exercício 5/72 alguns dados que serão necessários para esta resolução.

v B = 4,38 m s

ω = 3,23   r a d / s

Feito isto, fazer um esboço do mecanismo com os dados.

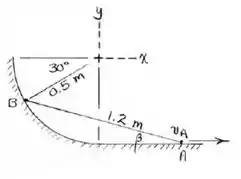
Por relações geométricas, podemos calcular o ângulo β :

s e n β = 0,5 - 0,5 c o s 30 ° 1,2 = 0,056 → β = 12 °

Este ângulo vai nos ajudar a decompor os vetores posição.

Aplicando a equação da aceleração relativa nos pontos B e A temos:

a B = a A + ( a B / A ) t + ( a B / A ) n

a B = a A + α × r B A - ω 2 r B A

a B = 0 + α k ^ × r B A (   - c o s 12 ° i ^ + s e n 12 ° j ^ ) - 3,23 2 ( 1,2 ) (   - c o s 12 ° i ^ + s e n 12 ° j ^ )

a B = - 0,25 α i ^ + 12,28 i ^ - 1,17 α j ^ - 2,6 j ^

Passo 2

Neste passo vamos ver o pulo do gato nessa questão.

O ponto B da barra está se movendo seguindo a trajetória circular do chão. Desta forma, a aceleração de B a B pode ser também escrita na forma de ( a B ) t + ( a B ) n , porém em relação ao centro deste círculo. Veja o desenho:

Portanto, reescrevendo a equação encontrada no passo 1:

a B t s e n 30 ° i ^ - c o s 30 ° j ^ + 4,38 2 0,5 c o s 30 ° i ^ + s e n 30 ° j ^ = - 0,25 α i ^ + 12,28 i ^ - 1,17 α j ^ - 2,6 j ^

Decompondo nas direções i ^   e   j ^ :

1 2 a B t + 33,3 = - 0,25 α i ^ + 12,28 i ^

- 3 2 a B t + 19,2 = - 1,17 α j ^ - 2,6 j ^

Resolvendo o sistema, temos que:

a B t = - 23,9   m / s 2

α = - 36,2 r a d / s 2

Resposta

a B t = - 23,9   m / s 2

α = - 36,2 r a d / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sabendo que, nos instantes mostrados nas figuras, a barra AB tem uma velocidade angular constante de 4 rad/s e uma aceleração angular de 2 rad/s², ambas no sentido horário, determine a aceleração angu
O tambor de 150 mm de raio gira sem escorregar sobre uma correia que se move para a esquerda com uma velocidade constante de 300 mm/s. No instante em que a velocidade e a aceleração do centro D do tam
Sabendo que, nos instantes mostrados nas figuras, a barra AB tem uma velocidade angular constante de 4 rad/s no sentido horário, determine a aceleração angular (a) da barra BD, (b) da barra DE.
Sabendo que, no instante mostrado na figura, a barra AB tem uma aceleração angular nula e uma velocidade angular constante de ω 0 no sentido horário, determine (a) a aceleração angular do braço DE, (b
Sabendo que, nos instantes mostrados nas figuras, a barra AB tem uma velocidade angular constante de 4 rad/s no sentido horário, determine a aceleração angular (a) da barra BD, (b) da barra DE.