Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.6 - Ex. 141

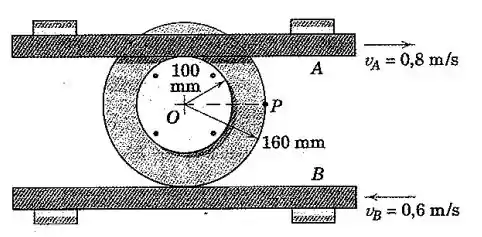
O mecanismo do Prob.5/75 é reapresentado aqui. Cada uma das barras deslizantes A e B se acopla sem deslizar na sua respectiva borda das duas rodas rebitadas. Se, além da informação apresentada, a barra A possui uma aceleração de 2m/s² para a direita e não há nenhuma aceleração da barra B, calcule o módulo da aceleração de P para o instante representado.

Passo 1

Então galera, nesse exercício tem mais uma vez (mesmo que de forma mais indireta) rolamento sem deslizamento. Na verdade, são 2 rolamentos. A ideia é primeiro encontrar a aceleração do centro das rodas para depois ficar mais fácil calcular a aceleração de P.

Vamos esboçar o mecanismo com os dados do enunciado.

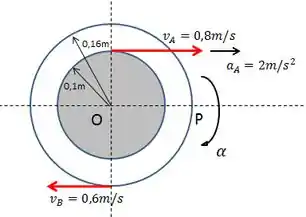
A partir daí, podemos usar alguns conceitos para calcular umas incógnitas. Como somente o ponto A está acelerado e B é um ponto de rolamento sem deslizamento, podemos calcular a aceleração angular da roda:

a A = α × r A B → 2 i ^ = - 0,26 α   i ^

α = - 7,69   k ^   r a d / s 2

Podemos também calcular a aceleração do ponto O:

a O = α × r O B = 1 , 23 i ^   m / s 2

Outro dado que será útil é a velocidade angular da roda:

v B = v A + ω × r A B

ω = - 0,6 - 0,8 0,26 = - 5 , 38 k ^   r a d / s

Passo 2

Bom, calculados esses importantes dados, podemos passar para a parte da aceleração relativa entra P e O:

a P = a O + a P / O n + a P / O t

Sabemos que a componente normal pode ser calculada como:

a P / O n = - r P / O ω 2 = - 0,16 - 5,38 2 = - 4,64 i ^   m / s 2

E ainda que a componente tangencial vale:

a P / O t = α × r P O = - 7,69 k ^ × 0,16 i ^ = - 1,23 j ^   m / s 2

Voltando para a equação da aceleração relativa:

a P = 1,23 i ^ - 4,64 i ^ - 1,23 j ^ = - 3,41 i ^ - 1,23 j ^   m / s 2

Por fim, o enunciado pede o módulo:

a P = - 3,41 2 + - 1,23 2 = 3,62   m / s 2

Resposta

a P = 3,62   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

15.159. Resolva o Problema 15.158 admitindo que a placa gire em torno de O com velocidade angular constante , no sentido horário.
15.160. No instante mostrado na figura, o comprimento da lança AB está sendo diminuído a uma taxa constante de 0,2 m/s e a lança está sendo baixada a uma taxa constante de 0,08 rad /s. Determine (a) a
15.161. No instante mostrado na figura, o comprimento da lança AB está sendo aumentado a uma taxa constante de 0,2 m/s e a lança está sendo baixada a uma taxa constante de 0,08 rad /s. Determine (a) a
A placa retangular mostrada na figura gira à taxa constante ω 2 = 12r a d / s em relação ao braço A E , que, por sua vez, gira à taxa constante ω 1 = 9r a d / s em torno do eixo Z . Para a posição mos
Resolva o Problema 15.222, considerando que, no instante mostrado, a velocidade angular ω 1 da placa de 10r a d / s está decrescendo a uma taxa de 25r a d / s 2 , enquanto a velocidade relativa u do p