Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 117

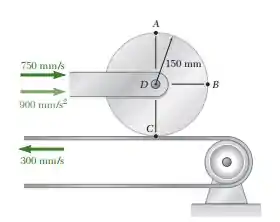
O tambor de 150 mm de raio gira sem escorregar sobre uma correia que se move para a esquerda com uma velocidade constante de 300 mm/s. No instante em que a velocidade e a aceleração do centro D do tambor estão indicadas, determine as acelerações A, B e C do tambor.

Passo 1

Vamos lá resolver mais essa. A velocidade do ponto D será igual a velocidade do tambor, v D = 750   m m / s . O ponto C, que está em contato com a correia, tem a velocidade v C = 300   m m / s . Antes de determinar a aceleração dos pontos A, B e C, vamos calcular a velocidade e a aceleração angular do tambor. Analisando a velocidade de C em relação a D, temos:

v C = v D + v C / D

- 300 i → = 750 i → - ω k → × - C D j → = 750 i → - 150 ω i →

- 300 = 700 - 150 ω → ω = 1050 150 = 7   r a d / s

Passo 2

A aceleração do ponto D é igual a aceleração do centro, a D = 900   m m / s 2 . Como o tambor não desliza, o ponto C tem somente uma componente vertical para a aceleração. Avaliando a aceleração de C em relação a D:

a → C = a → D + a → C / D t + a → C / D n

a C j → = 900 i → - α k → × - C D j → - ω 2 - C D j → = 900 i → - 150 α i → + 150 ω 2 j →

Igualando as coordenadas de cada lado da equação:

0 = 900 - 150 α → α = 6 r a d / s 2

a C = 150 ⋅ 7 2 = 7350   m m / s 2   = 7,35   m / s 2

Passo 3

Agora, vamos calcular as acelerações dos pontos A e B:

a → A = a → D + a → A / D t + a → A / D n

a → A = 900 i → - 6 k → × 150 j → - 7 2 150 j → = 900 i → + 900 i → - 7350 j →

a → A = 1800 i → - 7350 j →

a A = 1800 2 + - 7350 2 = 7570   m m / s 2   = 7,57   m / s 2

a → B = a → D + a → B / D t + a → B / D n

a → B = 900 i → - 6 k → × 150 i → - 7 2 150 i → = 900 i → - 900 j → - 7350 i →

a → A = - 6450 i → - 900 j →

a B = 6450 2 + - 90 0 2 = 6510   m m / s 2   = 6,51   m / s 2

Resposta

a A = 7,57 m/s²; a B = 6,51 m/s²; a C = 7,35 m/s²

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O punção, reapresentado aqui a partir do Prob. 5/57, é acionado por um movimento harmônico do setor articulado dado por θ = θ O s e n 2 π t . Pelo método dessa seção, calcule a aceleração do punção qu
Determine a aceleração angular da barra AB e a aceleração linear de A para θ = 90 °s eθ ˙ = 0eθ ¨ = 3 r a d / s 2 nessa posição. Desenvolva sua solução usando notação vetorial.
O conjunto eixo e roda do Prob. 5/102 é reapresentado aqui com a especificação adicional de que a aceleração do Centro O é de 1,4m / s 2 para a esquerda conforme mostrado. Se o eixo rola sobre a super
Determine a aceleração do pistão do Exemplo 5/15 para (a) θ = 0 ° ,b θ = 90 °ec θ = 180 ° . Considere o sentido positivo da direção x para a direita.
A configuração mostrada é projetada para produzir a oscilação do recipiente de pequenas peças em torno de C, como parte de um processo de produção. Obtenha uma expressão para a aceleração angular α do