Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.6 - Ex. 143

O mecanismo de implantação para a lança do magnetometro da nave espacial do Prob. 5/87 é novamente apresentado aqui. O elemento de acionamento OB possui uma velocidade angular constante no sentido horário ω O B de 0,5 rad/s quando cruza a posição vertical. Determine a aceleração angular α C A da lança para a posição mostrada onde tan ⁡ θ = 4 / 3 .

Passo 1

Primeiramente, vamos precisar de algumas informações do exercício 5/87. Vamos a elas:

ω A B = - 0,214 k ^ r a d s

ω C A = - 0,429   k ^ r a d s

Agora, vamos esboçar o mecanismo e adicionar algumas informações importantes.

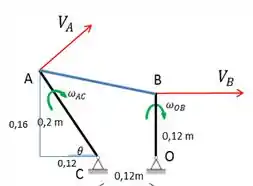
A partir da barra BO, podemos calcular a aceleração de B:

a B = - r O B ω O B 2 = - 0,12 × 0,5 2 = - 0,03 j ^   m / s 2

A partir da barra CA, podemos calcular a aceleração de A:

a A = a A / C n + a A / C t

a A = ω C A × ω C A × r C A + α C A × r C A

a A = 0,459 2 k ^ × k ^ × - 0,12 i ^ + 0,16 j ^ + α C A k ^ × - 0,12 i ^ + 0,16 j ^

a A = 0 , 1837 0,12 i ^ - 0,16 j ^ + α C A ( - 0,16 i ^ - 0,12 j ^ )

Em relação à barra AB, podemos calcular a componente normal:

a A / B n = ω A B × ω A B × r A B = 0,214 2 k ^ × k ^ × ( - 0,24 i ^ + 0,04 j ^ )

a A / B n = 0,0459 + 0,24 i ^ - 0,04 j ^ m / s 2

E sua componente tangencial:

a A / B t = α A B × r A B = α A B   k ^ × ( - 0,24 i ^ + 0,04 j ^ )

a A / B t = - 0,04 α A B i ^ - 0 , 24 α A B j ^   m / s 2

Agora, falta relacionar as acelerações dos pontos A e B. Então bora:

a A = a B + a A / B n + a A / B t

Substituindo os valores encontrados acima na equação:

0,1837 0,12 i ^ - 0,16 j ^ + α C A - 0,16 i ^ - 0,12 j ^ = - 0,03 j ^ + 0,0459 + 0,24 i ^ - 0,04 j ^ - 0,04 α A B i ^ - 0,24 α A B j ^

Temos que ter muito cuidado pra não se perder no meio de tanto número. Vamos decompor nas direções   i ^   e   j ^ para facilitar:

0,1837 0,12 i ^ + α C A - 0,16 i ^ = + 0,0459 + 0,24 i ^ - 0,04 α A B i ^

0,1837 - 0,16 j ^ + α C A - 0,12 j ^ = - 0,03 j ^ + 0,0459 - 0,04 j ^ - 0,24 α A B j ^

Resolvendo o sistema:

0,2757 = - α A B + 4 α C A

0,0204 = - 2 α A B + α C A

α C A = 0,0758   k ^   r a d / s 2

α A B = 0,0277   k ^   r a d / s 2

Resposta

α C A = 0,0758   k ^   r a d / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A BC é soldada a um braço que gira em torno de A com velocidade angular constante w. Na posição mostrada, a haste DE está sendo movida para a esquerda a uma velocidade constante u = 16 finis em relaçã
Um trenó de foguete é testado em uma pista reta construída ao longo de um meridiano. Sabendo que a pista está localizada na latitude 40 ° norte, determine a aceleração de Coriolis do trenó quando ele
O movimento do bico D é controlado pelo braço AB. No instante mostrado, o braço está girando no sentido anti-horário a uma taxa constante w = 2,4 rad / s e a porção BC está sendo estendida a uma taxa
Resolva o Problema 15.221, supondo que no instante mostrado a velocidade angular ω 1 da haste é 3 rad / s e está aumentando a uma taxa de 12 rad / s², enquanto a velocidade relativa u do colar é 34 in
O guindaste mostrado gira a uma taxa constante col = 0,25 rad / s; simultaneamente, a lança telescópica está sendo abaixada a uma taxa constante ω 2 = 0.40 r a d / s . Sabendo que, no instante mostrad