Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 11.Problemas de Revisão - Ex. 130

A barra de aço A B C de 12   m m de diâmetro foi dobrada na forma mostrada na figura. Sabendo que E = 200   G P a e G = 77,2   G P a , determine a deflexão da extremidade C provocada pela força de 150   N .

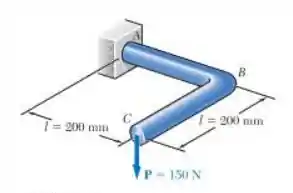
Passo 1

Fala, galerinha. Beleza? Bora pra mais um exercício.

Primeiro, vamos determinar o momento polar de inércia:

J = π 2 c 4

Onde:

c = d 2 = 12 2 = 0,006   m

Portanto, o momento polar de inercia vai ser:

J = π 2 0,006 4 J = 2,0358 × 10 - 9   m 4

E então, o momento de inercia vai ser:

I = 1 2 J I = 1,0179 × 10 - 9   m 4

Passo 2

Em seguida, vamos determinar a energia de deformação para cada porção da barra de aço. Para a porção A B , temos que o momento fletor vai ser:

M = - P x

Logo, temos que a energia de deformação na curvatura vai ser:

U A B , b = ∫ 0 L A B M 2 2 E I d x = P 2 2 E I ∫ 0 L A B x 2   d x

Substituindo:

U A B , b = P 2 L A B 3 6 E I = 150 2 200 × 10 - 3 3 6 200 × 10 9 1,0179 × 10 - 9 U A B , b = 0,14736   J

E para a energia de deformação para a torção, temos:

U A B , t = T 2 L 2 G J = P 2 L B C 2 L A B 2 G J U A B , t = 150 2 200 × 10 - 3 2 200 × 10 - 3 2 77,2 × 10 9 2,0358 × 10 - 9 U A B , t = 0,57265   J

Agora, vamos determinar a energia de deformação para a porção B C . O momento fletor vai ser:

M = - P x

Logo, temos que a energia de deformação na curvatura vai ser:

U B C = ∫ 0 L B C M 2 2 E I d x = P 2 2 E I ∫ 0 L A B x 2   d x

Substituindo:

U B C = P 2 L B C 3 6 E I = 150 2 200 × 10 - 3 3 6 200 × 10 9 1,0179 × 10 - 9 U B C = 0,14736   J

Passo 3

Por fim, vamos lembrar que a a energia de deformação é uma grandeza escalar, portanto, a máxima energia de deformação vai ser a soma das energias de deformação. Fica assim:

U = U A B , b + U A B , t + U B C U = 0,86737   J

Portanto:

1 2 P   δ = U δ = 2 U P = 2 0,86737 150 δ = 11,57   m m

É isso, galera Bora pra próxima?

Resposta

δ = 11,57   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na treliça mostrada, todos os membros são feitos do mesmo material e têm seções transversais uniformes, com as áreas indicadas. Determinar a energia de deformação da treliça, quando a carga P é aplica
Levando em conta somente o efeito das tensões normais, determinar a energia de deformação da viga prismática A B para o carregamento mostrado.
Assumindo que a viga prismática A B tem uma seção transversal retangular, mostrar que, para o carregamento dado, o máximo valor da densidade de energia de deformação na viga é u m = 15 U V onde U é a
Levando em conta somente o efeito das tensões normais, determinar a energia de deformação da viga prismática A B para o carregamento mostrado.
Levando em conta somente o efeito das tensões normais, determinar a energia de deformação da viga prismática A B para o carregamento mostrado.