Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 109
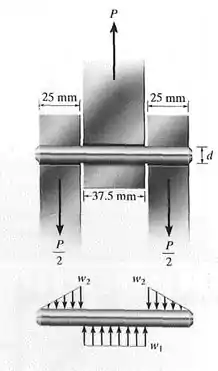
O pino está submetido a cisalhamento duplo, visto que é usado para interligar os três elos. Devido ao desgaste, a carga é distribuída nas partes superior e inferior do pino como mostra o diagrama de corpo livre. Determine o diâmetro do pino se a tensão de cisalhamento admissível for e a carga . Determine também as intensidades das cargas .
Passo 1
Bora lá, o que nós queremos com essa questão aqui? desejamos encontrar o diâmetro do pino que atravessa os elos, dadas as tensões de cisalhamento admissíveis dadas por
e o valor de . No caso desse problema como já temos uma notação a seguir, vamos utilizar. Primeiramente vamos utilizar as equações de equilíbrio das forças (o somatório das forças em determinada direção deve dar zero) para encontrarmos os valores de que também nos são pedidos pelo enunciado.
Passo 2
Dessa forma, vamos verificar o somatório das forças ao longo do eixo (vertical) para os pinos e para os elos, assim, teremos começando pelos pinos
Agora de forma análoga para os elos vamos ter
Passo 3
Agora, meus cheiros, ficou tranquilo terminar o nosso exercício e por quê? Bom, desejamos encontrar o valor de e para isso vamos utilizar a fórmula da tensão de cisalhamento dada por
Contudo devemos observar a figura com calma, pois temos um cisalhamento duplo e neste caso temos duas áreas que estão sendo cisalhadas, desta forma deve-se utilizar a seguinte fórmula.
Bora abrir a expressão da nossa área pro nosso aparecer, lembrando que nossa área é dada por:
Substituindo em vamos encontrar
Cara saca só essa dica que vale mais do que barras de ouro
1 MPa = 1 N/mm²
70 MPa = 70 N/ mm²
Então vamos deixa a tensão nessa notação 70 KN/ mm pois daí facilmente teremos a unidade do diâmetro, então partiu!!!!!!!!!!!
Pronto, acabou o problema.
Ahhhhh... mas você pode estar pensando: uai... mas por que ta diferente do gabarito??
Então... provavelmente em alguma outra edição ou na hora de traduzirem mudaram o valor de P. Se a gente fizer os cálculos com dá o gabarito certinhoo.