Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 47
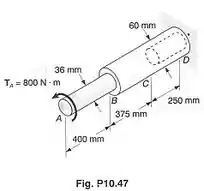
A barra de alumínio é fortemente ligada à barra de latão . Sabendo-se que a porção da barra de latão é vazada e tem um diâmetro interno de , determinar a energia de deformação total das duas barras.
Passo 1
Oi, galera bonita! Como estão? Tudo certinho? Espero que sim!
Bora fazer uma questão de energia de deformação pra dominar a matéria? Show, vamos lá!
Nesse exercício precisamos calcular a energia de deformação total das barras (de alumínio), e (de latão). Essa energia de deformação total é a soma entre a energia de deformação da barra , a energia de deformação da barra e a energia de deformação da barra
A figura abaixo mostra os dados que temos para calcular .
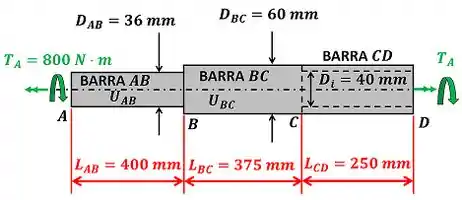
e são os diâmetros das barras e respectivamente. é o diâmetro interno da barra . , e são os comprimentos das barras , e respectivamente. é o torque que torce as barras.
Como o torque que torce todas as barras é constante e igual a , calculamos as energias de deformação , e das barras , e através da equação 10.22 do livro. Essa equação serve para barras com áreas constantes e torques constantes, como é nosso caso.
, e são os módulos de elasticidade transversais dos materiais das barras. Eles valem:
Agora que temos todas essas fórmulas, vamos começar a fazer as contas, calculando os momentos de inércia polares , e !
Passo 2
Antes de achar as energias de deformação , e de cada barra, temos que encontrar os valores dos momentos de inércia polares , e de cada barra
Achamos e , através das fórmulas de momentos de inércia polares para áreas circulares abaixo. Antes, devemos converter os diâmetros de pra , multiplicando eles por .
Como a barra é vazada, sua fórmula é diferente!
Essa barra tem um diâmetro interno e um diâmetro externo .
A fórmula de momento polar para áreas de seção transversal vazadas se encontra abaixo.
Não se esqueça de converter os diâmetros de pra , multiplicando eles por .
Com , e já podemos calcular as energias de deformação de cada barra no próximo passo!
Passo 3
Substituímos , e nas equações de , e para achar as energias de deformação. No entanto, antes disso converter o de para , multiplicando por e os comprimentos de pra , multiplicando eles por .
Somando essas três energias de deformação, conseguimos achar a energia de deformação total que a questão pede!
Show de bola! Finalizamos a questão! :)