Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 46
Os torques mostrados são exercidos nas polias , e . Sabe-se que ambos os eixos são maciços e feitos de latão , determinar a energia de deformação no: eixo ; eixo .
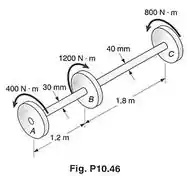
Passo 1
Como vão, pessoal? Tudo certinho? Vamos fazer uma questão de energia de deformação pra dominar a matéria? Então bora!
Nesse exercício precisamos calcular a energia de deformação das barras e .
Vamos chamar a energia de deformação da barra de e a energia de deformação da barra de . A figura abaixo mostra os dados que temos para calcular e .
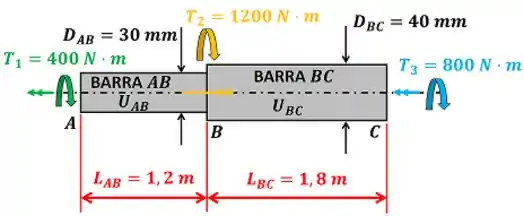
e são os diâmetros das barras e respectivamente. e são os comprimentos das barras e respectivamente. , e são os torques que torcem as barras.
Para calcular as energias de deformação e das barras e , precisamos usar a equação 10.22 do livro que serve para barras com áreas constantes e torques constantes.
é o módulo de elasticidade transversal do material da barra. Ele vale segundo o enunciado. e são os torques que agem nas barras e respectivamente.
Agora que temos todas essas fórmulas, vamos começar a fazer as contas, calculando e !
Passo 2
Vamos calcular quanto valem o torque . Achamos esse valor, cortando a barra no ponto e usando a equação de equilíbrio de momento na parte esquerda da barra. Essa equação diz que a soma de todos os torques deve ser igual a zero.
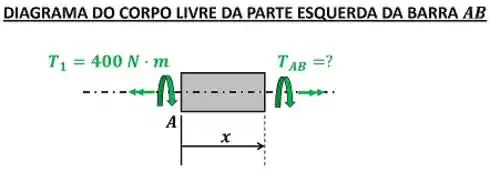
Calculamos , dizendo que a soma desses torques vale zero, porque a barra está parada.
Como o torque faz a barra girar para o sentido contrário (setinha verde do torque está pra esquerda), colocamos um sinal de menos na frente desse torque.
Com esse valor de torque, falta apenas calcular os valores de momento de inércia para achar .
Passo 3
Nesse passo vamos calcular e para resolver a letra (a) da questão!
Primeiro, achamos , através da fórmula de momentos de inércia polar para áreas circulares abaixo. Antes, devemos converter os diâmetros de pra , multiplicando eles por .
Agora sim podemos achar !
No entanto, antes disso converter o de para , multiplicando por .
Passo 4
Iniciamos a letra (b) da questão, calculando o torque .
Para calcular usamos o mesmo método. Só que agora temos que cortar a barra em um ponto que inclui o torque . O resto fica igual! Vamos achar através do equilíbrio de momento da parte esquerda da barra.
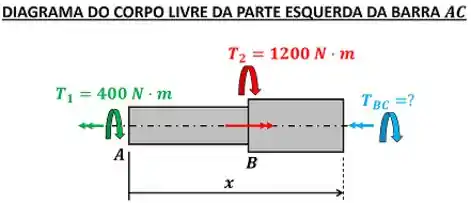
Como os torques e fazem a barra girar para o sentido contrário (setinha verde do torque está pra esquerda), colocamos um sinal de menos na frente desses torques.
No próximo passo vamos calcular e e acabar com a questão!
Passo 5
Vamos resolver logo a letra (b)! Primeiro, devemos achar com a equação abaixo!
Não se esqueça! Antes, devemos converter os diâmetros de pra , multiplicando eles por .
Com já podemos calcular a energia de deformação !
Aeeeee! Chegamos na resposta! Uhuul!