Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 3.Problemas - Ex. 38

A barra de alumínio   A B G = 27   G P a está ligada a barra de latão B D G = 39   G P a . Sabendo que a parte CD da barra de latão é vazada e tem um diâmetro interno de 40 mm, determine o ângulo de torção em A.

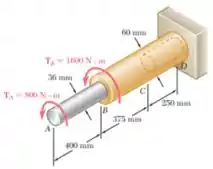
Passo 1

Para encontrarmos o ângulo de torção em A precisamos calcular eixo por eixo o torque, raio e o ângulo de torção de cada um deles.

Eixo AB

G = 27   G P a   = 27 × 10 9 P a

L =   0.400   m

T = 800   N / m

c = 1 2 d = 1 2 0.036   m = 0.018   m

J = π 2 c 4 = π 2 0.018 4 = 164.896 × 10 - 9 m 4

ϕ A B = T L G J = 800 0.400 27 × 10 9 164.896 × 10 - 9 = 71.875 × 10 - 3 r a d

Passo 2

Na seção BC temos:

G = 39   G P a   = 39 × 10 9 P a

L =   0.375   m

T = 800 + 1600 = 2400   N / m

c = 1 2 d = 1 2 0.060   m = 0.030   m

J = π 2 c 4 = π 2 0.030 4 = 1.27234 × 10 - 6 m 4

ϕ B C = T L G J = 2400 0.375 39 × 10 9 1.27234 × 10 - 6 = 18.137 × 10 - 3 r a d

Passo 3

Na seção Parte CD

L =   0.250   m

c 1 = 1 2 d 1 = 1 2 0.040   m = 0.020   m

c 2 = 1 2 d 2 = 1 2 0.060   m = 0.030   m

J = π 2 c 1 4 - c 2 4 = π 2 0.030 4 - 0.020 4 = 1.02102 × 10 - 6 m 4

ϕ C D = T L G J = 2400 0.250 39 × 10 9 1.02102 × 10 - 6 = 15.068 × 10 - 3 r a d

Passo 4

Agora temos o ângulo de torção em A.

ϕ A = ϕ A B + ϕ B C + ϕ C D = 71.875 × 10 - 3 + 18.137 × 10 - 3 + 15.068 × 10 - 3 = 105.080 × 10 - 3   r a d

ϕ C = 105.080 × 10 - 3 180 π = 6.02 °

Resposta

6.02 ° .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma placa anelar de latão G = 39G P a de espessura t = 6,36m m é usada para conectar o eixo de latão A B , de comprimento L 1 = 50m m e raio r 1 = 30m m , ao tubo de latão C D de comprimento L 2 = 250
Uma placa anelar de latão G = 39G P a de espessura t = 6,36m m é usada para conectar o eixo de latão A B , de comprimento L 1 = 50m m e raio r 1 = 30m m , ao tubo de latão C D de comprimento L 2 = 250
Desenvolver uma expressão aproximada para o ângulo de torção de um eixo, de forma de tronco de cone no Prob 3.56, substituindo o tronco de cone por n eixos cilíndricos de iguais comprimentos e raios r
Um torque T é aplicado como mostrado a um tronco de cone maciço AB. Mostrar por integração que o ângulo de torção em A é: ϕ A = 7 T L 12 π G c 4
Um eixo maciço e um eixo vazado são feitos de mesmo material e têm o mesmo peso e o mesmo comprimento. Expressando por n a reção c 1 / c 2 , mostrar que a relação T m / T v , entre o torque T m do eix