Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 123

Resolva o Problema 2.122, considerando que a = 180 m m .

Passo 1

E ai gurizada tudo belezinha? O enunciado pede que a gente determine primeiramente o deslocamento permanente do ponto C e depois a tensão residual da barra, então vamos começar a esboçar o diagrama de corpo livre.

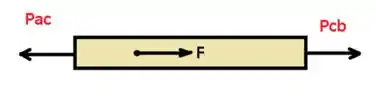
Sabendo que a área do elemento é: A = 1200 m m ² = 1200 x 10^(- 6) m ² , temos que determinar então a força exercida na barra

Força para ceder parte AC temos

P_A C = A sigma_Y = (1200 x 10^(- 6)) x (250 x 10^(- 6)) = 300 x 10^3 N

Para equilíbrio temos que realizar o somatório das forças na horizontal:

F + P_C B - P_A C = 0 P_C B = P_A C - F = 300 x 10^3 - 520 x 10^3 = - 220 x 10^3 N

E o alongamento é dado por:

delta_C = - (P_C B L_C B)/(E A) = ((220 x 10^3) x (0,440 - 0,120))/((200 x 10^9) x (1200 x 10^(- 6))) = 0,29333 x 10^(- 3) m

E agora podemos determinar a tensão no eixo CB vem comigo :D sigma_C B = (P_C B)/(A) = (220 x 10^3)/(1200 x 10^(- 6)) = 183,333 x 10^6 P a

Passo 2

Galera calma não desistam de mim, é cansativo, é mas vale a pena 😉 , considere que:

delta^'_C = (P^'_A C L_A C)/(E A) = - (P^'_C B L_C B)/(E A) = ((F - P^'_A C) x L_C B)/(E A)

Sendo que as forças nas seções podem ser obtidas da seguinte forma: P^'_A C ((L_A C)/(E A) + (L_C B)/(E A)) = (F L_C B)/(E A)

Calculando para a seção AC e CB temos:

P^'_A C = (F L_C B)/(L_A C + L_C B) = ((520 x 10^3) x (0,440 - 0,180))/(0,440) = 307,27 x 10^3 N P^'_C B = P^'_A C - F = 307,27 x 10^3 - 520 x 10^3 = - 212,73 x 10^3 N

delta '_C = ((307,27 x 10^3) x ( 0,180 ))/((200 x 10^9) x (1200 x 10^(- 6))) = 0,23045 x 10^(- 3) m

Agora podemos determinar a tensão e o alongamento em C: sigma^'_A C = (P^'_A C)/(A) = (307,27 x 10^3)/(1200 x 10^(- 6)) = 256,068 x 10^6 P a

sigma^'_C B = (P^'_C B)/(A) = (- 212,73 x 10^3)/(1200 x 10^(- 6)) = - 177,275 x 10^6 P a

Para as demais temos:

  1. delta_C , p = delta_C - delta '_C = 0,23833 x 10^(- 3) - 0,23045 x 10^(- 3) = 0,00788 x 10^(- 3) m
  2. sigma_A C , r e s = sigma_A C - sigma^'_A C = 250 x 10^6 - 256,058 x 10^6 = - 6,0580 x 10^6 P a sigma_C B , r e s = sigma_C B - sigma^'_C B = - 183,333 x 10^6 + 177,275 x 10^6 = - 6,0580 x 10^6 P a

Resposta

  1. = 0,00788 m m
  2. = - 6,06 M P a = - 6,06 M P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um bloco de peso W é colocado em contato com uma viga em um certo ponto D e liberado. Mostre que a deflexão máxima resultante no ponto D é duas vezes maior do que a deflexão provocada por uma força es
Cada elemento da treliça é mostrada é feito de aço e tem uma área de seção transversal conforme apontado. Usando E = 29 × 10 6p s i , determine a energia de deformação .
O anel D é liberado do repouso na posição mostrada, e o seu movimento é interrompido por uma pequena placa fixada à extremidade C da barra vertical A B C . Determine a massa do anel para o qual a tens
Dois eixos sólidos de aço são conectados pelas engrenagens mostradas. Utilizando o método do trabalho e energia, determine o ângulo de rotação que descreve a extremidade em D quando T = 820N ∙ m . Uti
Para a viga prismática mostrada, determine a inclinação no ponto D .