Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas de Revisão - Ex. 129

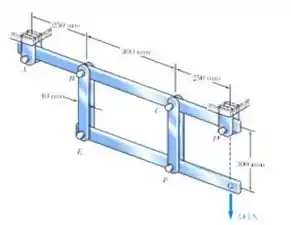
Cada uma das quatros barras verticais que conectam os dois elementos horizontais rígidos é feita de alumínio ( E = 70   G P a ) e tem seção transversal retangular e uniforme 10 x 40 mm. Para o carregamento mostrado, determine o deslocamento de (a) ponto E, (b) ponto F e (c) ponto G.

Passo 1

E ai gurizada tudo belezinha? O enunciado pede que a gente determine o deslocamento no ponto E, ponto F e ponto G. Antes vamos desenhar o diagrama de corpo livre, vem comigo :D:

Agora podemos determinar o somatório do momento em F

+ ∑ M F = F x d = 0

    - 400   x   2 F B E - 250   x   24 = F B E = - 7,5   k N = - 7,5   x   10 3 N

E também o somatório do momento em E :D + ∑ M E = f x d = 0

    - 400   x   2 F C F - 650   x   24 = 19,5   k N = 19,5   x   10 3 N

Gurizada agora precisamos determinar a área

A = 10   x   40 = 400   m m 2 = 400   x   10 - 6 m ²

Considerando o comprimento: L = 300   m m = 0,300   m podemos determinar os seguintes alongamentos :D

δ B E = F B E L E A = - 7,5   x   10 3   x   0,300 70   x   10 9   x   400   x   10 - 6 = - 80,357   x   10 - 6 m   δ C F = F C F L E A = 19,5   x   10 3   x   0,300 70   x   10 9   x   400   x   10 - 6 = 208,93     x   10 - 6 m

Passo 2

Galera considere esse diagrama de corpo livre que leva em consideração os alongamentos e o ângulo , vejam 0/

  1. Deflexão do ponto E. δ E = δ B F
  2. Deflexão do ponto F. δ F = δ C F

    3. Deixei θ seja pequena mudança no ângulo de inclinação.

    θ = δ E + δ F L E F = 80,357   x   10 - 6 + 208,93   x   10 - 6 0,400 = 723,22   x   10 - 6   r a d i a n o s

  3. Deflexão do ponto G.

δ G = δ F + L F G θ δ G = δ F + L F G θ = 208,93   x   10 - 6 + 0,250   x   723,22   x   10 - 6 = 389,73   x   10 - 6 m  

Resposta

  1. δ E = 80,4   μ m   ↑
  2. δ F = 290   μ m   ↓
  3. δ G = 390   μ m   ↓
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra de aço A B C tem seção transversal quadrada com 19,05m m de lado e é submetida a uma carga P de 222,4k N .Usando E = 200G P a , determine a flexão no ponto C .
Um disco de raio a foi soldado à extremidade B do eixo de aço de seção cheia A B . Um cabo é enrolado ao redor do disco e uma força vertical P é aplicada à extremida C do cabo. Sabendo que o raio do e
A barra de aço A B C de 12m m de diâmetro foi dobrada na forma mostrada na figura. Sabendo que E = 200G P a e G = 77,2G P a , determine a deflexão da extremidade C provocada pela força de 150N .
Uma haste uniforme de rigidez à flexão E I é carregada conforme mostrado. Determine ( a ) a deflexão horizontal no ponto D , ( b ) a declividade do ponto D .
A barra de aço CD, com 20mm de diâmetro está soldada ao eixo de aço AB também com 20 mm de diâmetro conforme mostrado. A extremidade C da barra CD toca a superfície rígida mostrada quando um conjugado