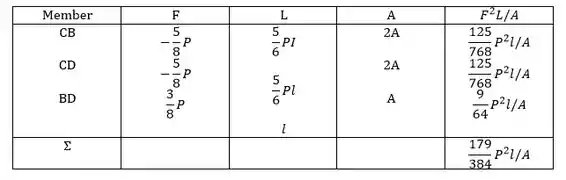
Na treliça mostrada, todos os elementos são feitos do mesmo material e têm a área da seção transversal indicada. Determine a energia de deformação da treliça quando lhe é aplicada a força P.

Passo 1
E ai gurizada tudo bem? O enunciado pede que a gente determine a energia de deformação da treliça quando lhe é aplicada a força P, vamos começar esboçando o diagrama de corpo livre :D
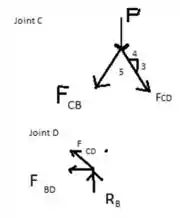
Passo 2
Fazendo o somatório das forças em x temos:
Fazendo o somatório das forças em y temos:
Passo 3
Agora determinar as forças em x e y na horizontal :D