Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 74
Para uma barra submetida a um carregamento axial, expressar a deformação especifica normal , na direção que forma um ângulo de 45°C com o eixo do carregamento, em termos da deformação especifica axial por:
- Comparação das hipotenusas dos triângulos indicados na , que representam um elemento, antes e depois, da deformação;
- Usando os valores das correspondentes tensões e indicadas na , e a lei de generalizada.
Passo 1
No item A queremos saber quanto vale a deformação especifica da nossa diagonal, e para isso o enunciado é bem claro em pedir esse cálculo através de elementos, por isso podemos fazer a seguinte suposição de cálculo:
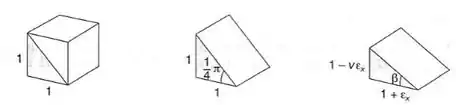
Fazendo os elementos, teremos que:
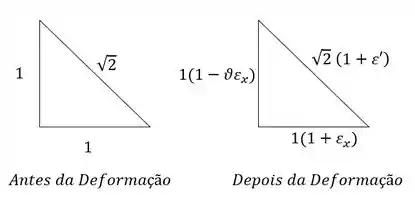
E queremos definir exatamente a deformação relativa à hipotenusa que é definido por . Usando Pitágoras teremos que:
Todos os elementos ao quadrado serão menores, logo podemos desprezar esses elementos que serão muito pequenos, sendo assim teremos que:
Passo 2
Sabemos que o nosso elemento infinitesimal sujeito ao estado plano de tensões é dado por:
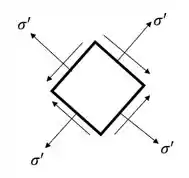
Sabemos que a lei de hooke é dada por:
E a nossa figurinha é:
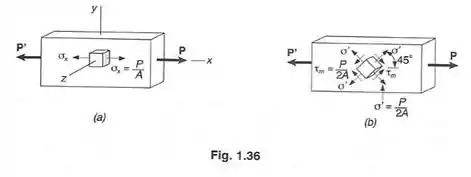
Sabemos que:
Substituindo temos que:
Sabemos que:
E sabemos que:
Assim podemos substituir e teremos que:
Assim temos que a nossa deformação será:
E assim definimos as deformações.