Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 60
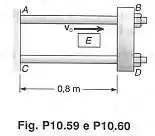
O bloco de está com uma velocidade quando bate perpendicularmente à placa que está presa na extremidade das barras e , de diâmetros iguais a . Sabendo-se que as barras são feitas de um aço para o qual e , determinar a máxima velocidade permissível , para que as barras não fiquem permanentemente deformadas.
Passo 1
Fala, lindonas e lindões! Muitas dúvidas em resistência dos materiais? Então vamos fazer essa questão de carregamento produzido por impacto para tirar todas elas!
A questão quer saber com qual velocidade máxima o bloco pode se chocar sem deformar permanentemente as barras. Para fazer o cálculo dessa situação, precisamos igualar a máxima energia de deformação que cada barra pode ter sem se deformar permanentemente à parte da energia cinética do bloco que cada barra vai absorver individualmente no choque.
Como é máxima energia que uma das barras pode absorver, ela pode ser calculada multiplicando a máxima energia específica que a barra pode absorver pelo volume da barra. Além disso, é calculada através da equação 10.8 do livro.
Como é a energia que cada uma das barras absorve durante o choque, ela é igual à metade da energia cinética que o bloco tem, quando colide. Logo:
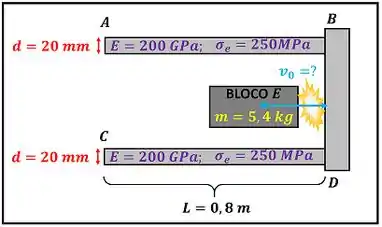
A figura abaixo mostra os dados que temos para calcular a velocidade máxima do bloco .
Pronto! Agora temos todas as informações que precisamos para calcular . Então vamos fazer isso no próximo passo.
Passo 2
Vamos começar os cálculos definindo quanto vale .
Para isso, precisamos lembrar que o volume de uma barra cilíndrica depende do diâmetro da barra. Por isso, antes de usar a fórmula de , precisamos converter de pra , multiplicando seu valor por .
Para usar a fórmula de temos que passar de para , multiplicando o valor por e temos que converter de para , multiplicando por .
Pronto, enfim podemos substituir os dados na fórmula.
Agora vamos partir para o cálculo de .
Passo 3
Para achar , precisamos saber quanto vale a velocidade do bloco. Mas podemos substituir o valor de e calcular quanto vale em função de .
Substituindo e na primeira, somos capazes de achar o valor da velocidade máxima do bloco.
Uhuuuul! Mais uma questão resolvida! Tá voando, heim?!