Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 74

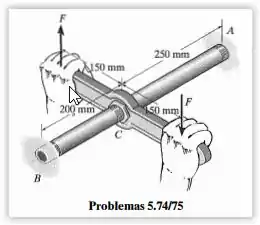
O tubo de bronze C 86100 tem diâmetro externo de 37,5   m m e espessura de 0,3   m m . A conexão C está sendo apertada com uma chave de torque. Se o torque desenvolvido em A for 16   N . m , determine o valor   F das forças conjugadas. O tubo está engastado na extremidade B .

Passo 1

O problema quer saber qual a força conjugada que é aplicada no sistema. Um fato muito útil para esse problema é que a extremidade B e a extremidade A são engastadas, logo ϕ B / A = 0 . O torque desenvolvido em A é uma das reações do momento, M F , provocado pelas forças F .

Como não ocorre variação de T , J ou G o ângulo de torção é dado por:

ϕ = T L J G

O enunciado nos fornece:

T A C = 16   N ⋅ m

L F C = 0,15   m

L B C = 0,2   m

L A C = 0,25   m

Aço A-36, portanto, G a ç o = 75 ⋅ 10 9   P

Passo 2

Devemos realizar o somatório dos momentos para determinar a força F . Observando a imagem a seguir podemos ter uma ideia melhor de como fica o somatório.

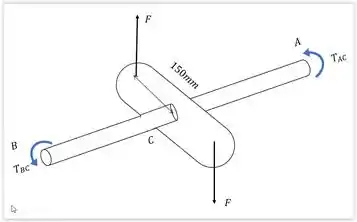
Como é possível notar, o momento provocado pelas forças conjugadas é somado entre si, resultando num momento de sentido oposto ao dos torques em A e B . Temos assim.

⟲ +     ∑ T = 0

T B C + T A C - M F = 0

T B C + 16 - 2 ⋅ ( F ⋅ 0,150 ) = 0

T B C + 16 = F ⋅ 0,3

Para determinar T B C podemos igualar os ângulos de torção em A e em B . Teremos então:

ϕ A = ϕ B

T A C L A C J G = T B C L B C J G

T A C L A C = T B C L B C

16 ⋅ 0,25 = T B C ⋅ 0,2

T B C = 20   N . m

Sendo assim:

T B C + 16 = F ⋅ 0,3

20 + 16 = F ⋅ 0,3

F = 120   N

Resposta

F = 120   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O eixo sólido mostrado é feito de um aço baixo carbono considerando elastoplástico com G = 77,2G P a e t E = 145M P a . determine o ângulo de giro produzido pela aplicação de um torque de intensidade
O eixo composto mostrado consiste em uma jaqueta de latão de 5.08 mm de espessura ( G l a t ã o = 39G P a ) ã unido a um núcleo de aço de 40 mm de diâmetro G a ç o = 77.2G P a ç . As tensões de cisalh
Dois eixos de aço sólidos são ajustados com flanges que em seguida são conectadas por parafusos como mostrado. Os parafusos são ligeiramente subdimensionados de modo que permitam uma rotação relativa
Os cilindros de seção transversal cheia AB e BC estão conectados em B e engastados em suportes fixos de A e em C. Sabendo os módulos de rigidez são 77,2 GPa para o alumínio e 38.6 GPa para o latão, de
Para o eixo de seção circular do Problema 3.94, determine o ângulo de giro causado pela aplicação de um torque de intensidade (a) T = 80k i p ⋅ i n e (b) T = 130k i p ⋅ i n .